Classes de Thom-Boardman - Définition
La liste des auteurs de cet article est disponible ici.
Classes ΣI (Boardman, 1967)
On doit à Boardman une extension intéressante des classes ΣI(f). Ces classes, notées ΣI, où
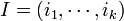
Codimension de ΣI
La codimension νI(m,n) de ΣI, où
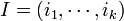
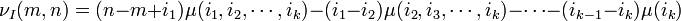
où
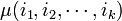
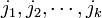
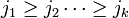
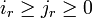
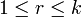
Tableau des classes pour les petites dimensions
On donne ici les classes non vides pour les petites valeurs de m = dimM et n = dimN. Pour chaque classe, on écrit entre crochets sa codimension et sa dimension: ΣI[ν,m − ν]. On note Reg l'ensemble des points réguliers: Reg=
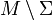
![\begin{array}{|c|l|l|l|} \hline & & & \Sigma^0 [0,3]= \mathrm{Reg} \\ n=3 & \Sigma^0 [0,1]= \mathrm{Reg} & \Sigma^0 [0,2]= \mathrm{Reg} & \Sigma^{1,0}[1,2] \\ & & \Sigma^{1}[2,0] & \Sigma^{1,1,0}[2,1] \\ & & & \Sigma^{1,1,1}[3,0] \\ \hline & & \Sigma^0 [0,2]= \mathrm{Reg} & \Sigma^1 [0,3]= \mathrm{Reg} \\ n=2 & \Sigma^0 [0,1]= \mathrm{Reg} & \Sigma^{1,0}[1,1] & \Sigma^{2,0} [2,1] \\ & & \Sigma^{1,1}[2,0] & \Sigma^{2,1} [3,0] \\ \hline n=1 &\Sigma^0[0,1]=\mathrm{Reg} & \Sigma^1[0,2] = \mathrm{Reg} & \Sigma^2[0,3] = \mathrm{Reg} \\ & \Sigma^1[1,0] & \Sigma^2[2,0] & \Sigma^3[3,0] \\ \hline & m=1 & m=2 &m=3 \\ \hline \end{array}](https://static.techno-science.net/illustration/Definitions/autres/2/2dd2dea48027887b8ca5d0977b77d21e_c835d49174cefa9bfaea0d7e6c989e19.png)

















































