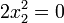Classes de Thom-Boardman - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Introduites par René Thom en 1956, et généralisées par J.M. Boardman en 1967, les classes de Thom-Boardman Σ sont un outil pour l'étude des singularités des applications différentiables
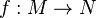
Classes ΣI(f) (Thom, 1956)
Etant donnée une application (indéfiniment) différentiable
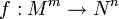
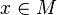
Un point
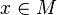
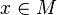
Le cas général est défini inductivement en posant, pour toute famille d'entiers
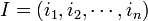
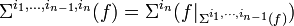
On a les inclusions
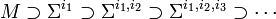
Application à l'optique géométrique
Les caustiques de l'optique géométrique sont modélisées mathématiquement en tant que singularités, ou plus exactement en tant que singularités lagrangiennes. La théorie des singularités lagrangiennes montre qu'il existe 5 types génériques de points caustiques dans notre espace physique: les plis A2, les fronces A3, les queues d'aronde A4, les ombilics hyperboliques
Le lien avec les singularités d'applications différentiables vient de la remarque suivante. Considérons un ensemble (ou congruence) de rayons lumineux. Chaque rayon est défini par deux paramètres x1, x2, qui sont par exemple les coordonnées du point Q du front d'onde W d'où est issu le rayon. Pour décrire tous les points P du système des rayons, on ajoute aux coordonnées x1 et x2 une troisième coordonnée x3 le long du rayon, par exemple la distance QP mesurée le long du rayon (x1,x2). On définit ainsi une application f qui fait correspondre au triplet (x1,x2,x3) le point (y1,y2,y3) de l'espace physique, situé à la coordonnée (distance) x3 le long du rayon (x1,x2). Dire que les rayons "se croisent", c'est dire que f n'est pas injective. La non surjectivité de f exprime l'existence de zones d'ombres. La caustique K du système de rayons est l'ensemble singulier Σ de f, ou plus exactement son image dans l'espace physique: K = f(Σ).
Cette modélisation des rayons par une application différentiable f explique que la caustique se compose d'une surface-pli A2 = Σ1(f), de lignes-fronces A3 = Σ1,1(f), et de points queues d'arondes A4 = Σ1,1,1(f). Elle n'explique cependant pas la présence des ombilics
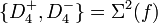
La caractérisation des points caustiques par les classes de Thom-Boardman permet leur calcul effectif dans la plupart des applications.
Exemples de calculs de ΣI(f)
Points réguliers
Soit la fonction
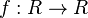
Le pli
Soit la fonction
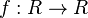
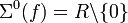
La fronce
Soit l'application
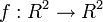
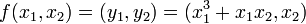
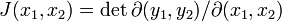
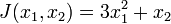
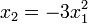
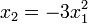

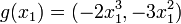
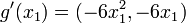
La queue d'aronde
Soit l'application
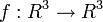
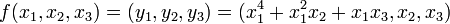
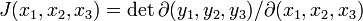
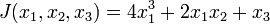
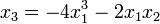
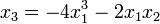
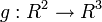
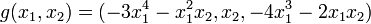
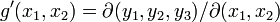
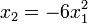
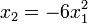
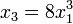
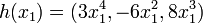
Les ombilics
Soit l'application
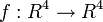
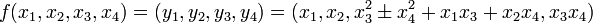
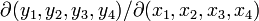
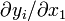
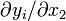
L'ombrelle de Whitney-Cayley
Soit l'application
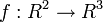
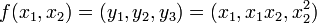
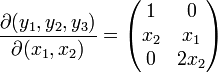
Σ1(f) est obtenu en annulant les 3 mineurs d'ordre 2 soit: x1 = 0, 2x2 = 0,