Code cyclique - Définition

Définition

• Un code linéaire sur F_d et de paramètres [n, k, δ] est dit cyclique si l'espace vectoriel est muni de la structure d'anneau F_d/P[X], avec P[X] = Xⁿ - 1, et si le code C est un idéal de dimension k de distance minimale δ.

Dire que le code est un idéal revient à dire qu'il est cyclique, c’est-à-dire qu'il vérifie la propriété suivante :

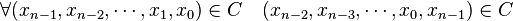
Dans ce cas, la longueur du code est toujours une puissance du cardinal du corps de base moins un. Dans la pratique, la longueur du code est une puissance du cardinal du corps, souvent égal à deux et le dernier bit est un bit de parité.

On suppose dorénavant que C est un code cyclique de paramètres [n, k, δ] sur le corps F_d et qu'il existe m tel que d ^m - 1 est égal à n, α désigne une racine primitive de l'extension F_{n + 1} de F_d.

Implémentation

Matrice génératrice

Contrôle