Code cyclique - Définition

Code cyclique et code parfait

Distance minimale et code binaire

Le Minitel 1, sorti en 1982

Dans le cas des codes binaires, les polynômes cyclotomiques d'indice n à coefficients dans F₂ engendrent des codes cycliques parfaits, de distance minimale égale à trois. Ce type de code est adapté pour les petites perturbations relativement fréquentes. Chaque mot peut comporter une unique erreur, elle sera corrigée. Un code de cette nature est, par exemple utilisé pour le minitel, c'est un code BCH sur 17 octets.

La théorie de Galois assure que l'extension F_n de F₂ possède un élément primitif α, et donc F_n est égal à F₂[α]. L'élément α est générateur du groupe multiplicatif, son polynôme minimal est donc un polynôme cyclotomique Φ_n[X] d'indice n sur F_d. Son degré est égal à m car α est un élément primitif.

Ce polynôme remplit les conditions d'optimalité.

• L'idéal C engendré par Φ_n[X] est un code cyclique.

De plus :

• L'idéal C engendré par Φ_n[X] possède les paramètres suivant [2^m - 1, 2^m - m - 1, 3].

Le code associé est donc un code binaire de Hamming. Ce résultat est vrai uniquement parce que le code est binaire. Considérons par exemple F₂₇ = F₃[α] où α est un générateur primitif de l'extension. L'ordre de α est égal à 26, donc α¹³ est une racine carrée de l'unité, différente de 1. α¹³ est donc égal à -1. Le polynôme X¹³ - 1 admet α pour racine, c'est donc un multiple de son polynôme cyclotomique et il est élément du code. Pourtant son poids est égal à deux.

Ce sont donc les spécificités de la caractéristique 2 qui assurent la véracité de la proposition.

• L'idéal C engendré par Φ_n[X] est code parfait.

Dans le cas général, la borne de Singleton (cf code linéaire) n'est pas atteinte. Considérons en effet, le cas où m est égal à 7. La longueur n du code est égale à 127, la dimension k du code à 120 et la distance minimale δ à trois. On en déduit:

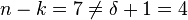
• L'idéal C engendré par Φ_n[X] est un code cyclique.

Les polynômes cyclotomiques, pour les corps de caractéristique finis, ne sont pas toujours les mêmes que ceux du même indice sur les nombres rationnels. Par exemple, pour sur F₂, le polynôme cyclotomique d'indice 127 possède comme corps de décomposition le corps F₁₂₈ de dimension 7 sur F₂. Tout polynôme cyclotomique d'indice 127 est donc de degré sept. Sur les nombres rationnels, comme 127 est premier, le polynôme cyclotomique est de degré 126. Sur F₂ il en existe 18, tous de degré 7 et dont le produit s'identifie au polynôme cyclotomique de même indice à coefficients sur les entiers.

Montrer que C est un code cyclique revient à montrer que Φ_n[X] est un diviseur de Xⁿ - 1. Si (α_i) est un représentant de chaque classe de conjugaison (cf le paragraphe Polynôme minimal et corps fini de l'article Endomorphisme de Frobenius) à m éléments, l'égalité suivante montre la relation de divisibilité recherchée:

Ce qui achève la démonstration.

• La distance minimale δ de l'idéal C engendré par Φ_n[X] est au moins égale à 3, si le code est binaire.

Considérons un polynôme Q[X] de F_d[X] ayant exactement deux monômes à coefficients non nuls et ayant α pour racine:

Comme α est racine du polynôme Q[X], l'égalité α^k = 1 est vérifiée. Comme α est un élément primitif du groupe cyclique F_n^* k est un multiple de d ^m - 1. En conséquence, l'image du polynôme Q[X] dans l'espace vectoriel est nulle. Cela signifie que l'espace vectoriel ne contient aucun mot de code ayant un poids égal à deux.

De plus, les seuls monômes ayant α pour racine sont ceux ayant une puissance multiple de son ordre multiplicatif égal à n - 1, leurs images dans l'espace vectoriel sont donc encore nulles.

• L'idéal C engendré par Φ_n[X] est code parfait si le code est binaire.

Soit P le supplémentaire du code composé par tous les polynômes de degré strictement inférieur à m, S la boule de centre le vecteur nul et de rayon 1 et φ l'application de S dans P qui à un polynôme associe son reste par la division euclidienne par le polynôme Φ_n[X]. L'application est linéaire, elle est injective car si deux polynômes ont même image par φ leur différence est un mot de code ayant un poids égal à deux ou à 0. Comme aucun mot de code n'a de poids égal à deux d'après le paragraphe précédent, leur différence est nécessairement nulle. P et S ont même cardinaux, égal à n + 1 c’est-à-dire 2^m. En effet S contient n monômes et le polynôme nul, et P est un espace vectoriel de dimension m. L'application φ est donc une bijection.

Considérons l'ensemble des boules de rayon 1 pour la distance de Hamming. Le paragraphe précédent montre qu'elles sont toutes disjointes. Il suffit alors de démontrer que tout polynôme est élément d'une de ces boules. Soit Q[X] un polynôme quelconque et R[X] le reste de sa division euclidienne par Φ_n[X]. R[X] est élément de P, il existe un élément M[X] de S, c’est-à-dire un polynôme de poids égal à 0 où à 1, tel que φ(R[X]) = M[X]. En effet, φ est une bijection de S dans P. Le polynôme Q[X] - M[X] est un mot de code, car ses deux facteurs ont même reste par la division euclidienne par Φ_n[X]. Comme le poids de M[X] est inférieur ou égal à un, on a montré que Q[X] est à une distance inférieure ou égale à 1 d'un mot de code. Q[X] est donc dans une boule de centre un élément du code et de rayon 1. Ce qui achève la démonstration.

• La distance minimale δ de l'idéal C engendré par Φ_n[X] est au moins plus égal à 3, si le code est binaire.

Si le paramètre δ est plus grand que trois, alors il existe au moins un élément qui n'est dans aucune boule de centre un mot du code et de rayon 1. Or la proposition précédente démontre que l'ensemble de ces boules forme une partition de l'espace vectoriel. Ce qui prouve l'impossibilité et achève la démonstration.

 

Code BCH

Si le contexte précédent possède de nombreuses applications industrielles, il présente néanmoins des limitations justifiant l'utilisation d'autres méthodes.

La solution précédente s'appuie sur les propriétés de la caractéristique 2. Il peut être utile d'utiliser d'autres corps finis que ceux multiple de deux. Cette contrainte est d'importance relativement faible dans l'industrie, les codes binaires sont en effet largement répandus.

En revanche, une telle approche ne permet que la résolution d'une unique erreur dans un mot. Cette limitation n'est pas compatible avec, par exemple, le cahier des charges des disques compacts. Un disque compact peut subir des rayures ou être localement recouvert d'une poussière. Une suite de lettres erronées peut posséder une longueur égale à 4.096.

La théorie des corps finis permet néanmoins de proposer une solution MSD c’est-à-dire qui atteint la borne de Singleton. Elle se fonde sur un calcul réalisé la première fois par le mathématicien Vandermonde pour résoudre l'équation cyclotomique dans le cas de la caractéristique zéro. Ce calcul reste d'actualité pour les corps finis.

Dans la suite du paragraphe Δ désigne un entier tel que 1 < Δ < n + 1 et β désigne un élément de F_n+1 tel que ses Δ premières puissances soit toutes distinctes

• Un polynôme à coefficients dans F_d dont Δ puissances successives et distinctes de β sont racines et sans racine multiple, engendre un code cyclique C dont la distance minimale δ est supérieure ou égale à Δ + 1.

Remarque:La propriété du paragraphe précédent est une conséquence de cette proposition. En effet, les propriétés de l'automorphisme de Frobenius démontre que si α est racine du polynôme cyclotomique, alors α² l'est aussi dans le cas des corps binaires.

Cette proposition est à la base d'une famille de codes dit code BCH (pour Bose, Ray-Chaudhuri, Hocquenghem)

• Un Code BCH de longueur prescrite Δ est un code cyclique à coefficients dans F_d et de longueur n tel qu'il existe un entier b et dont le polynôme générateur G vérifie l'égalité suivante. Si b est égal à un 1 le code est dit BCH au sens strict.

Ici Φ_i[X] désigne le polynôme cyclotomique ayant αⁱ pour racine.

Un code BCH ne permet pas, en général, la génération de codes parfaits. Considérons l'extension binaire de dimension 7 et le code BCH au sens strict de longueur prescrite 5. Son polynôme générateur est le produit de deux polynômes de degré 7, celui ayant α comme racine (et donc aussi α² et α⁴) et celui ayant α³. Il corrige effectivement deux erreurs, mais la boule de centre 0 et de rayon 2 contient 1 + 127 + (127*126)/2 soit 8 129 points, alors qu'un supplémentaire du code est isomorphe à l'espace des polynômes de degré strictement inférieur à 14 soit 16 384. Les redondances sont plus de deux fois plus vastes que la boule de rayon deux.

Certains code BCH sont néanmoins parfaits. Considérons par exemple l'extension quadratique de F₃. Sa boule unité contient 1 + 26 éléments soit 27. Le polynôme cyclotomique de racine α contient α³ comme deuxième racine, celui contenant α² contient α⁶ comme deuxième racine et le produit des deux polynômes engendre un code de distance minimale 4 et peut donc corriger une unique erreur. Un supplémentaire est isomorphe à l'espace des polynômes de degré inférieur ou égal à 3, et contient donc 27 éléments, autant que la boule unité, le code est donc parfait.

• Un polynôme à coefficients dans F_d dont Δ puissances successives distinctes de β sont racines et sans racine multiple, engendre un code cyclique C dont la distance minimale δ est supérieure ou égale à Δ + 1.

Considérons un polynôme P[X] de poids de Hamming inférieur ou égal à Δ et élément du code.

Soit β^b, β^b+1, ..., β^b+Δ-1 la suite des Δ racines successives du polynôme générateurs. Puisque P[X] est un mot de code, il possède les éléments de la suite comme racine. Si l'on utilise les notations suivantes:

Les égalités P[β^b+i] = 0 deviennent:

Si A est le vecteur colonne de coefficients α_i et si B est la matrice de coefficients ζ_jⁱ. Les égalités précédentes s'écrivent sous forme matricielles: B.A = 0. Or B est la transposée d'une matrice de Vandermonde. Comme tous les ζ_j sont distincts, la matrice est inversible. Ceci démontre que A et le vecteur colonne nul, et donc les coefficients a _i sont tous nuls.

En conclusion, l'unique mot du code P[X] de poids inférieur ou égal à Δ est le polynôme nul. La proposition est donc démontrée.

 

Code de Reed-Solomon

Les CD utilisent un code de Reed-Solomon capable de corriger jusqu'à 4.096 bits erronés consécutifs

Si la propriété précédente ne permet pas d'obtenir assurément des codes MDS, l'approche BCH peut être enrichie pour pallier cette difficulté. Considérons par exemple le corps F₆₄. Il peut être vu comme l'extension quadratique de F₈. Alors d est égal à 8 et m à 2. L'espace vectoriel associé est un espace de dimension d ^m égal 63 sur F₈, soit une longueur de 189 en code binaire. Si α désigne un élément primitif du corps F₈, alors le polynôme G[X], défini par :

est un diviseur de X⁶³ - 1. L'idéal associé est donc un code cyclique C. Le théorème précédent montre que ce code possède une distance minimale de 9. Il admet comme paramètres [63, 55, 9]. C'est un code satisfaisant l'égalité de la borne du singleton (cf le paragraphe Borne du singleton et code MDS de l'article Code linéaire). Considéré comme un code binaire, il corrige jusqu'à 12 erreurs consécutives sur un code de dimension 189 et de longueur 175. Cette idée est à la base du code de Reed-Solomon.

• Un Code de Reed-Solomon de distance construite Δ avec 1 < Δ < n est un code BCH sur un corps F_n+1 de dimension n généré par un polynôme G[X] défini par:

La proposition du paragraphe précédent montre que :

• Un Code de Reed-Solomon de distance construite Δ sur F_n+1 possède pour paramètres [n, n - Δ + 1, Δ]. Un tel code est MDS.

Le code est MDS pour Minimum Distance Séparable si et seulement si la borne du singleton est atteinte.

Pour permettre de larges redondances avec une bonne optimalité, trois autres méthodes peuvent être ajoutées, le code raccourci, le code démultiplié et l'entrelacement. Le Code CIRC utilisé pour le disque compact est un code de Reed-Solomon sur le corps F₂₅₆ utilisant ces trois outils.