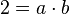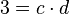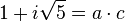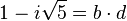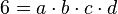Idéal - Définition

Introduction

En mathématiques, un idéal est une structure algébrique définie dans un anneau. Les idéaux généralisent de façon féconde l'étude de la divisibilité pour les entiers. Il est ainsi possible d'énoncer des versions très générales de théorèmes d'arithmétique tels que le théorème des restes chinois ou le théorème fondamental de l'arithmétique, valables pour les idéaux. On peut aussi comparer cette notion à celle de sous-groupe distingué pour la structure algébrique de groupe en ce sens qu'elle permet de définir la notion d'anneau quotient.

Aspect historique

La théorie des idéaux est relativement récente puisque elle fut créée par Richard Dedekind vers la fin du XIX^e siècle. À cette époque, une partie de la communauté mathématique s'intéresse aux nombres algébriques et plus particulièrement aux entiers algébriques.

La question est de savoir si les entiers algébriques se comportaient comme les entiers relatifs, en particulier la décomposition en facteurs premiers de manière unique. Il semblait bien, dès le début du XIX^e siècle, que cela n'était pas toujours le cas : 6 par exemple pouvant se décomposer dans l'anneau sous la forme ou sous la forme

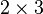
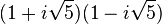
Ernst Kummer pressent alors que cela va dépendre des nombres en question et invente la notion de nombres complexes idéaux.

L'idée est de rendre unique la décomposition en facteurs premiers en ajoutant artificiellement d'autres nombres (de la même manière qu'on ajoute i aux nombres réels tel que i² = − 1 afin de disposer de nombres aux carrés négatifs). Dans l'exemple ci-dessus, on va "inventer" quatre nombres "idéaux" a, b, c et d tels que :

Ainsi, 6 se décomposera alors de manière unique en :

C'est Dedekind en 1871 qui reprend la notion de nombre idéal de Kummer et qui crée la notion d'idéal dans un anneau. Il s'intéresse principalement aux anneaux d'entiers algébriques, c'est-à-dire à des anneaux commutatifs, unitaires et intègres. C'est dans ce domaine que se trouvent les résultats les plus intéressants sur les idéaux. Il crée sur l'ensemble des idéaux d'un anneau commutatif, unitaire et intègre des opérations semblables à l'addition et la multiplication dans les entiers relatifs.

La théorie des idéaux a permis une avancée significative dans l'algèbre générale, mais aussi dans l'étude des courbes algébriques (géométrie algébrique).

Morphisme d'anneau

Un idéal joue, pour les anneaux, le même rôle que les sous-groupes normaux pour les groupes.

• Soit A et B deux anneaux et φ un morphisme de A dans B, alors le noyau de φ est un idéal bilatère.

• Soit A un anneau et I un idéal bilatère de A, alors le groupe quotient A/I peut être muni d'une unique structure d'anneau telle que la surjection canonique de A dans A/I soit un morphisme d'anneaux. Cf. section ci-dessous.

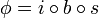
• Soit A et B deux anneaux, φ un morphisme d'anneau de A dans B. Notons s l'application canonique de A dans l'anneau quotient A/I et i le morphisme de φ(A) dans B qui à b associe b. Alors, i est une injection, s une surjection et il existe une bijection b tel que :

• Soit A et B deux anneaux et un morphisme d'anneau de A dans B. Alors:
  • Si J est un idéal bilatère de B alors est un idéal bilatère de A. Si, de plus, J est un idéal premier de B, alors est un idéal premier de A. Il n'y a en revanche pas de résultat analogue pour les idéaux maximaux.
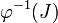
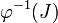
  • Si φ est un morphisme d'anneaux surjectif de A dans B, alors pour tout idéal bilatère I de A, φ(I) est un idéal bilatère de B.
  • La propriété ci-dessus n'est en général pas vraie si φ n'est pas surjectif. On peut prendre par exemple A=ℤ, B=ℚ et φ l'inclusion canonique. Alors φ(I) n'est un idéal de ℚ que si I est l'idéal nul.