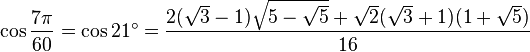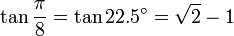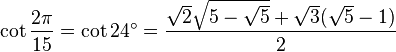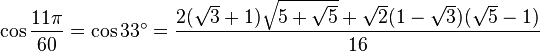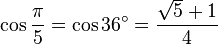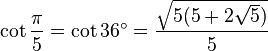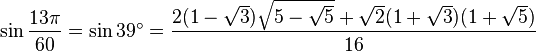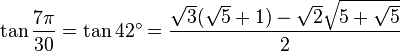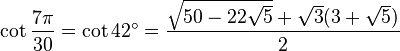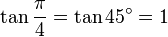Vendredi 4 Avril 2025
Rechercher 🔍

Constante trigonométrique exacte - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Table des constantes

Introduction

En mathématiques, les expressions de constantes exactes pour les expressions trigonométriques sont parfois très utiles, principalement pour la simplification des solutions en radicaux qui permettent des simplifications supplémentaires.

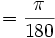
Toutes les valeurs de sinus, cosinus et tangente d'angles d'incrément de 3° sont dérivables en utilisant les identités : demi-angle, Double-angle, Addition/soustraction ainsi que les valeurs pour 0°, 30°, 36° et 45°. Note : 1° = \frac{\pi}{180}\, radians.

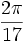
Cet article est incomplet dans au moins deux sens. D'abord, il est toujours possible d'appliquer la formule du demi-angle et trouver une expression exacte pour le cosinus d'un demi du plus petit angle de la liste. Ensuite, cet article exploite seulement les deux premiers des cinq nombres premiers de Fermat connu : 3 et 5. On pouvait en principe noter des formules impliquant les angles \frac{2\pi}{17}\, , \frac{2\pi}{257}\, , ou \frac{2\pi}{65537}\, , mais elles auraient été trop difficiles à manier pour la plupart des applications. En pratique, toutes les valeurs de sinus, cosinus et tangente absentes dans cet article sont approximées en utilisant les techniques décrites dans l'article Construire des tables trigonométriques.

Table des constantes

Les valeurs en dehors des angles 0° ... 45° sont trivialement extraites des axes du cercle unité par réflexion symétrie à partir de ces valeurs. (Voir Identité trigonométrique)

0° Fondamental

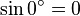
\sin 0^\circ = 0
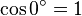
\cos 0^\circ = 1
\tan 0^\circ = 0

3° - Polygone à 60 côtés

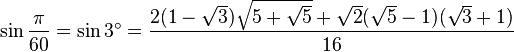
\sin \frac {\pi}{60} = \sin 3^\circ = \frac{ 2 (1 - \sqrt3) \sqrt{5 + \sqrt5} + \sqrt2 (\sqrt5 - 1) (\sqrt3 + 1) }{16}
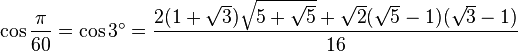
\cos \frac {\pi}{60} = \cos 3^\circ = \frac{ 2 (1 + \sqrt3) \sqrt{5 + \sqrt5} + \sqrt2 (\sqrt5 - 1) (\sqrt3 - 1) }{16}
\tan \frac {\pi}{60} = \tan 3^\circ = \frac{ \left( (2 - \sqrt3) (3 + \sqrt5) - 2 \right) \left(2 - \sqrt{2 (5 - \sqrt5)}\right) }{4}

6° - Polygone à 30 côtés

\sin \frac {\pi}{30} = \sin 6^\circ = \frac{(\sqrt6) \sqrt{5 - \sqrt5} - (\sqrt5 + 1)}{8}
\cos \frac {\pi}{30} = \cos 6^\circ = \frac{(\sqrt2) \sqrt{5- \sqrt5} + \sqrt3( \sqrt5+1)}{8}
\tan \frac {\pi}{30} = \tan 6^\circ = \frac{(\sqrt2) \sqrt{5 - \sqrt5} - \sqrt3(\sqrt5 - 1)}{2}
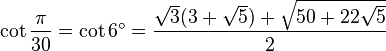
\cot \frac {\pi}{30} = \cot 6^\circ = \frac{\sqrt3 (3 + \sqrt5) + \sqrt{50 + 22 \sqrt5}}{2}

9° - Polygone à 20 côtés

\sin \frac {\pi}{20} = \sin 9^\circ = \frac{\sqrt2(\sqrt5 + 1) - 2\sqrt{5 - \sqrt5}}{8}
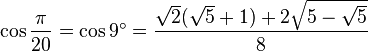
\cos \frac {\pi}{20} = \cos 9^\circ = \frac{\sqrt2(\sqrt5 + 1) + 2\sqrt{5 - \sqrt5}}{8}
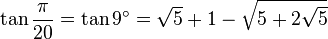
\tan \frac {\pi}{20} = \tan 9^\circ = \sqrt5 + 1 - \sqrt{5 + 2\sqrt5}
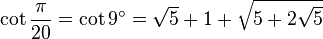
\cot \frac {\pi}{20} = \cot 9^\circ = \sqrt5 + 1 + \sqrt{5 + 2\sqrt5}

12° - Polygone à 15 côtés

\sin \frac{\pi}{15} = \sin 12^\circ = \frac{(\sqrt2) \sqrt{5 + \sqrt5} - \sqrt 3 (\sqrt 5 -1)}{8}
\cos \frac{\pi}{15} = \cos 12^\circ = \frac{(\sqrt6) \sqrt{5 + \sqrt5} + (\sqrt 5 - 1)}{8}
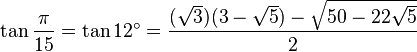
\tan \frac{\pi}{15} = \tan 12^\circ = \frac{(\sqrt3) (3 - \sqrt5 ) - \sqrt{50 - 22 \sqrt5}}{2}
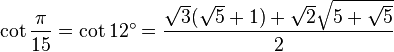
\cot \frac{\pi}{15} = \cot 12^\circ = \frac{\sqrt3 (\sqrt5 + 1) + \sqrt2 \sqrt{5 + \sqrt5}}{2}

15° - Polygone à 12 côtés

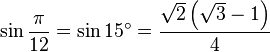
\sin \frac{\pi}{12} = \sin 15^\circ = \frac{\sqrt 2 \left(\sqrt 3 - 1\right)}{4}
\cos \frac{\pi}{12} = \cos 15^\circ = \frac{\sqrt 2 \left(\sqrt 3 + 1\right)}{4}
\tan \frac{\pi}{12} = \tan 15^\circ = 2 - \sqrt 3
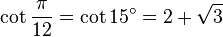
\cot \frac{\pi}{12} = \cot 15^\circ = 2 + \sqrt 3

18° - Polygone à 10 côtés

\sin \frac{\pi}{10} = \sin 18^\circ = \frac{\sqrt 5 - 1}{4}
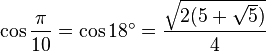
\cos \frac{\pi}{10} = \cos 18^\circ = \frac{\sqrt{2(5 + \sqrt 5)}}{4}
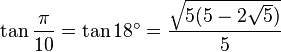
\tan \frac{\pi}{10} = \tan 18^\circ = \frac{\sqrt{5(5 - 2 \sqrt 5)}}{5}
\cot \frac{\pi}{10} = \cot 18^\circ = \sqrt{5 + 2 \sqrt 5}

20° - Ennéagone

\sin\frac{\pi}{9}=\sin 20^\circ=\sqrt[3]{-\frac{\sqrt{3}}{16}+\sqrt{-\frac{1}{256}}}+\sqrt[3]{-\frac{\sqrt{3}}{16}-\sqrt{-\frac{1}{256}}}=
2^{-\frac{4}{3}}(\sqrt[3]{i-\sqrt{3}}-\sqrt[3]{i+\sqrt{3}})
\cos\frac{\pi}{9}=\cos 20^\circ=
2^{-\frac{4}{3}}(\sqrt[3]{1+i\sqrt{3}}+\sqrt[3]{1-i\sqrt{3}})

21° - Somme 9° + 12°

\sin \frac{7\pi}{60} = \sin 21^\circ = \frac{2(\sqrt 3 + 1) \sqrt{5 - \sqrt 5} - \sqrt 2 (\sqrt 3 - 1) (1 + \sqrt 5)} {16}\,
\cos \frac{7\pi}{60} = \cos 21^\circ = \frac{2 (\sqrt 3 - 1) \sqrt{5 - \sqrt 5} + \sqrt 2 (\sqrt 3 + 1) (1 + \sqrt 5)} {16}\,
\tan \frac{7\pi}{60} = \tan 21^\circ = \frac{(1 + 2 \sqrt 3 - \sqrt 5) \sqrt{5 - 2 \sqrt 5} + (2 + \sqrt 3)(\sqrt 5 - 3) + 2} {2}\,

22,5° - Octogone

\sin \frac {\pi}{8} = \sin 22.5^\circ = \frac{\sqrt{2 - \sqrt{2}}}{2}
\cos \frac {\pi}{8} = \cos 22.5^\circ = \frac{\sqrt{2 + \sqrt{2}}}{2}
\tan \frac {\pi}{8} = \tan 22.5^\circ = \sqrt{2}-1
\cot \frac {\pi}{8} = \cot 22.5^\circ = \sqrt{2}+1

24° - Somme 12° + 12°

\sin \frac {2\pi}{15} = \sin 24^\circ = \frac{\sqrt3(\sqrt5 + 1) - \sqrt2 \sqrt{5 - \sqrt5}}{8}
\cos \frac {2\pi}{15} = \cos 24^\circ = \frac{\sqrt6 \sqrt{5 - \sqrt5} + \sqrt5 + 1}{8}
\tan \frac {2\pi}{15} = \tan 24^\circ = \frac{\sqrt{50 + 22 \sqrt5} - \sqrt3 (3 + \sqrt5)}{2}
\cot \frac {2\pi}{15} = \cot 24^\circ = \frac{\sqrt2 \sqrt{5 - \sqrt5} + \sqrt3(\sqrt5 - 1)}{2}

27° - Somme 12° + 15°

\sin \frac {3\pi}{20} = \sin 27^\circ = \frac{2 \sqrt{5 + \sqrt5} - \sqrt2(\sqrt5 - 1)}{8}
\cos \frac {3\pi}{20} = \cos 27^\circ = \frac{2 \sqrt{5 + \sqrt5} + \sqrt2(\sqrt5 - 1)}{8}
\tan \frac {3\pi}{20} = \tan 27^\circ = \sqrt5 - 1 - \sqrt{5 - 2 \sqrt5}
\cot \frac {3\pi}{20} = \cot 27^\circ = \sqrt5 - 1 + \sqrt{5 - 2 \sqrt5}

30° - Hexagone

\sin \frac{\pi}{6} = \sin 30^\circ = \frac{1}{2}
\cos \frac{\pi}{6} = \cos 30^\circ = \frac{\sqrt 3}{2}
\tan \frac{\pi}{6} = \tan 30^\circ = \frac{\sqrt 3}{3}
\cot \frac{\pi}{6} = \cot 30^\circ = \frac{3}{\sqrt 3} = \sqrt 3

33° - Somme 15° + 18°

\sin \frac{11\pi}{60} = \sin 33^\circ = \frac{2(\sqrt 3 - 1) \sqrt{5 + \sqrt 5} + \sqrt 2 (\sqrt 3 + 1) (\sqrt 5 - 1)} {16}
\cos \frac{11\pi}{60} = \cos 33^\circ = \frac{2 (\sqrt 3 + 1) \sqrt{5 + \sqrt 5} + \sqrt 2 (1 - \sqrt 3) (\sqrt 5 - 1)} {16}
\tan \frac{11\pi}{60} = \tan 33^\circ = \frac {(-15 + 10\sqrt 3 - 7\sqrt 5 + 4\sqrt{15} )\sqrt{5(5 - 2 \sqrt 5)} + 5(\sqrt 3 - 2)(3 + \sqrt 5) + 10}{10}

36° - Pentagone

\sin \frac{\pi}{5} = \sin 36^\circ = \frac{\sqrt{2(5 - \sqrt 5)} }{4}
\cos \frac{\pi}{5} = \cos 36^\circ = \frac{\sqrt 5+1}{4}
\tan \frac{\pi}{5} = \tan 36^\circ = \sqrt{5 - 2\sqrt 5}
\cot \frac{\pi}{5} = \cot 36^\circ = \frac{ \sqrt{5(5 + 2\sqrt 5)}}{5}

39° - Somme 18°+ 21°

\sin{\frac{13\pi}{60}} = \sin{39^\circ} = \frac{2(1-\sqrt 3)\sqrt{5-\sqrt 5} + \sqrt 2 (1 + \sqrt 3)(1 + \sqrt 5)}{16}
\cos{\frac{13\pi}{60}} = \cos{39^\circ} = \frac{2 (1+\sqrt 3)\sqrt{5-\sqrt 5} + \sqrt2(\sqrt 3 - 1)(\sqrt 5 + 1)}{16}
\tan{\frac{13\pi}{60}} = \tan{39^\circ} = \frac{\left(\sqrt{2(5+\sqrt 5)}-2\right)\left((2-\sqrt 3)(\sqrt 5 - 3) + 2\right)}{4}

42° - Somme 21° + 21°

\sin \frac {7\pi}{30} = \sin 42^\circ = \frac{ \sqrt6 \sqrt{5 + \sqrt5} - (\sqrt5 - 1)}{8}
\cos \frac {7\pi}{30} = \cos 42^\circ = \frac{ \sqrt2 \sqrt{5 + \sqrt5} + \sqrt3(\sqrt5 - 1)}{8}
\tan \frac {7\pi}{30} = \tan 42^\circ = \frac{ \sqrt3(\sqrt5 + 1) - \sqrt2 \sqrt{5 + \sqrt5}}{2}
\cot \frac {7\pi}{30} = \cot 42^\circ = \frac{ \sqrt{50 - 22 \sqrt5} + \sqrt3(3 + \sqrt5)}{2}

45° - Carré

\sin \frac{\pi}{4} = \sin 45^\circ = \frac{\sqrt 2}{2}
\cos \frac{\pi}{4} = \cos 45^\circ = \frac{\sqrt 2}{2}
\tan \frac{\pi}{4} = \tan 45^\circ = 1
\cot \frac{\pi}{4} = \cot 45^\circ = 1
- Introduction - Table des constantes
miniature
2
La NASA a découvert un effet inattendu de l'apesanteur 🦴
miniature
Des médicaments contre le cholestérol efficaces contre le cancer ? 💊
miniature
1
Darwin se serait trompé sur l'origine de la vie, voici pourquoi 🌍
miniature
Quand des robots-boules se coordonnent par le regard 👀
miniature
Découverte: certains poissons utilisent des outils 🛠
miniature
Pourquoi les personnes obèses éprouvent-elles moins de plaisir à manger ? 🧠
miniature
Les océans de la Terre n'avaient autrefois pas du tout la même couleur 🌊
miniature
Une cartographie inédite révèle la consommation énergétique du cerveau 🧠
miniature
Des chercheurs ont intercepté et décodé "facilement" des messages sous-marins depuis les airs ✈️
miniature
Voici pourquoi les femmes ressentent plus de douleur chronique que les hommes 🧐
miniature
Un immense iceberg se détache et révèle ce surprenant écosystème caché depuis des siècles 🦑
miniature
Un colibri imite une chenille pour survivre: découvrez cette stratégie étonnante 🐦
miniature
Cette forme de vie géante ne ressemble à rien d'autre de connu 🌎
miniature
Recherche: cette nouvelle molécule se montre terriblement efficace contre la calvitie 🔬
miniature
1
Des tardigrades génétiquement modifiés pour survivre... sur le Soleil ☀️
miniature
Or, cuivre... pourquoi ces métaux précieux se trouvent dans les zones de subduction ? 🌋
miniature
Une avancée majeure dans la supraconductivité à haute température 🌡️
miniature
Les chimpanzés fabriquent leurs outils comme des ingénieurs 🛠️
miniature
Mach 16: des surprises physiques découvertes dans les vols hypersoniques 🚀
miniature
Des scientifiques ont réussi à filmer la séparation des brins de l'ADN 🧬
miniature
Comment 13 degrés peuvent transformer une foule en chaos ? 🚶‍♂️
miniature
Découverte: les phoques savent évaluer la quantité d'oxygène dans leur sang 🤿
miniature
Les trous noirs pourraient-ils protéger la vie dans l'Univers ? 🌱
miniature
Implants mammaires en silicone: une toxicité remise en question
miniature
Découverte d'un "broyeur d'étoiles" dans notre galaxie 🌀
miniature
Neandertal et Sapiens: une collaboration inattendue il y a 100 000 ans 🤝
miniature
Que sont ces sphères noires découvertes sur Mars ? 🔴
miniature
Découverte: les champignons contre... la grippe 🍄
miniature
Découverte inédite: voici comment notre cerveau attache les souvenirs entre eux 🖇️
miniature
Découverte: les requins émettent des sons ! 🦈
miniature
Des scientifiques inventent un ciment qui aspire le CO2 🌎
miniature
Comment le cerveau décode le temps: du récit aux réseaux neuronaux 🕰️
miniature
Horloge atomique dans son smartphone et GPS 1000 fois plus précis ⏱️
miniature
L'ocytocine: l'hormone de l'amour ou simple mythe ? 💕
miniature
Cette nouvelle méthode permettrait d'identifier une vie extraterrestre inattendue 👽
miniature
Une araignée géante filmée dans les abysses de l'Antarctique 🕷️
miniature
Trois familles d'objets planétaires identifiées dans le Système Solaire externe 🔭
miniature
Découverte d'une griffe géante à 2 doigts appartenant à une nouvelle espèce de dinosaure 🦖
miniature
Un nouvelle technologie de vaisseaux nucléaires pour explorer le Système solaire 🚀
miniature
Votre cerveau se consomme lui-même pour rechercher de l'énergie, pendant un exercice intense 🏃
miniature
Des vestiges organiques découverts sur Mars 🧐
miniature
Pourquoi les armes nucléaires sont-elles si difficiles et dangereuses à produire ? 💥
miniature
MRAM: la mémoire informatique du futur enfin là ? ⚡
miniature
Vidange d'un lac glaciaire: la catastrophe du Sikkim en 2023 expliquée 🌊
miniature
1
Qu'est-ce qui a bien pu creuser ces tunnels il y a plusieurs millions d'années ? ⛏️
miniature
Les secrets biologiques de Maria Branyas Morera, la supercentenaire 🕰️
miniature
Exploiter la rotation terrestre pour produire de l'électricité: l'énergie verte de demain ? ⚡
miniature
Que nous apprennent ces émissions radioactives de météorites lunaires et martiennes ? ☢️
miniature
La Chine dévoile un processeur quantique fiable à 99.9% 🚀
miniature
Voici les emblématiques espèces éteintes que la science pourrait bientôt ressusciter 🦣
Page générée en 0.116 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise