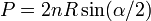Polygone - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
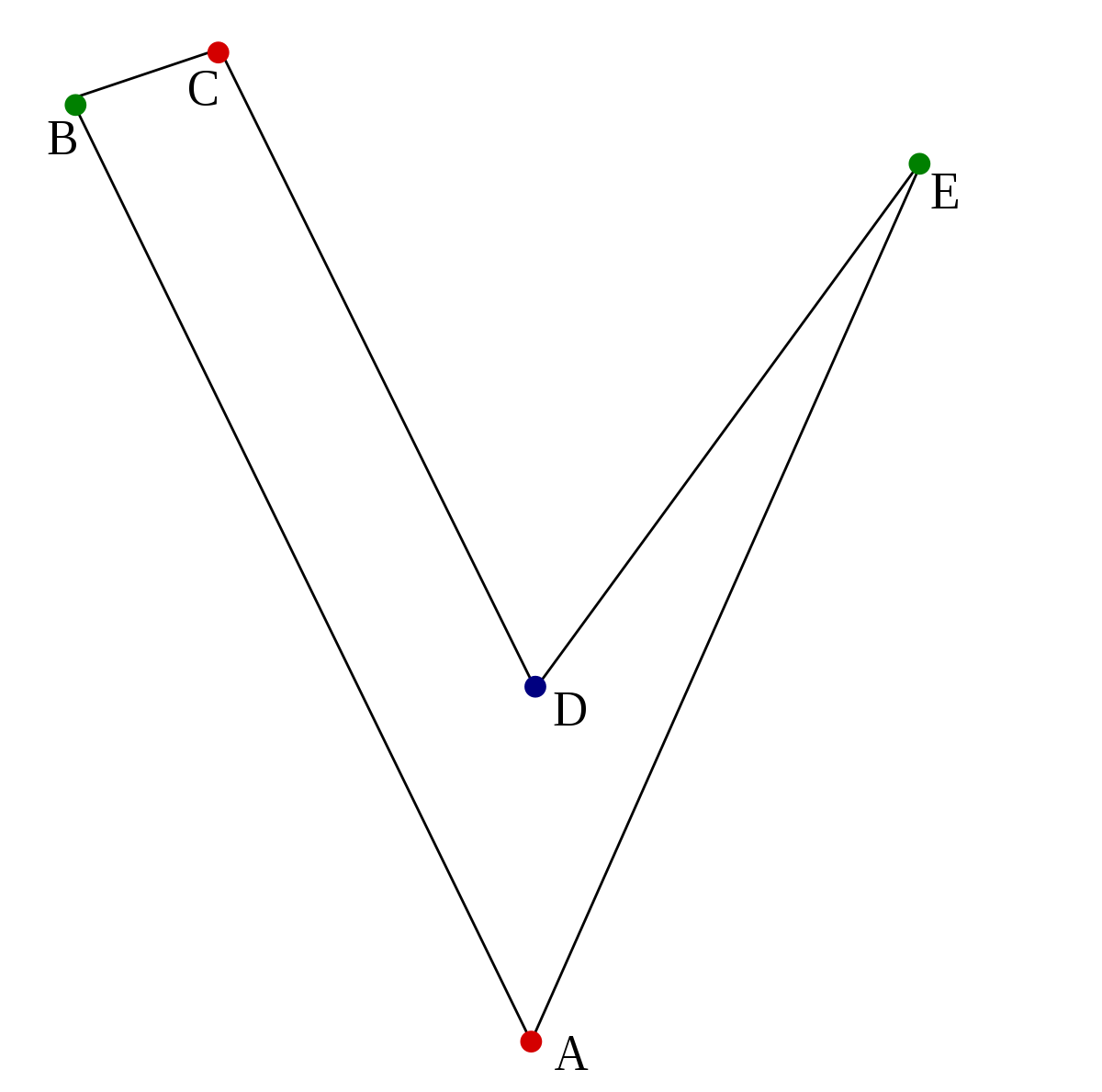
En géométrie euclidienne, un polygone (du grec polus, nombreux, et gônia, angle) est une figure géométrique plane, formée d'une suite cyclique de segments consécutifs et délimitant une portion du plan.
Il peut être convexe ou non, voire croisé si au moins deux côtés non consécutifs sont d'intersection non vide.
Lorsqu'un polygone n'est pas croisé, la somme de ses angles ne dépend que de son nombre de sommets.
Le bord d'un polygone est un cas particulier de ligne brisée.
La notion de polygone est généralisée en dimension supérieure par celles de polyèdre et de polytope.
Vocabulaire de base
Un polygone est constitué :
- d'une suite finie de points du plan appelés sommets ;
- des segments reliant les couples de sommets consécutifs ainsi que d'un segment reliant le premier et le dernier point, tous ces segments étant appelés côtés ;
- d'une partie ouverte et bornée du plan, appelée intérieur et dont la frontière est contenue dans la réunion des côtés.
Un polygone est en général désigné par la juxtaposition des lettres désignant les sommets, dans l'ordre de la suite.
L'ordre d'un polygone est le nombre de ses sommets.
La désignation d'un polygone en toute généralité s'écrit donc A1A2A3...An, constitué de n sommets et de n segments [A1A2], [A2A3]… [An − 1An] et [AnA1].
On dénomme alors polygone la figure notée « A1A2A3...An », et constituée par la suite des n segments : [A1A2], [A2A3], ... [An-1An] et [AnA1].
À chaque sommet est associé un angle, c'est l'angle entre les deux côtés qui aboutissent au sommet.
Ordre d'un polygone
Le nombre n des côtés d'un polygone est communément appelé ordre de ce polygone. C'est évidemment aussi le nombre de ses sommets ou celui de ses angles. Par exemple, un polygone d'ordre cinq détient cinq sommets, cinq angles et cinq côtés.
Eléments opposés
- Si l'ordre d'un polygone est pair :
-
-
- les sommets séparés par n/2 côtés sont dits « opposés » entre eux ;
- même chose pour les angles correspondants ;
- les côtés séparés par n/2 sommets sont dits eux aussi « opposés » entre eux.
-
- Si l'ordre du polygone est impair, les côtés sont « opposés » aux sommets et aux angles ( et vice versa ) ; plus précisément, chaque sommet ( ou chaque angle ) est « opposé » au côté situé (n - 1)/2 sommets plus loin.
Côtés prolongés et diagonales
Les droites qui portent les côtés d'un polygone sont appelées les côtés prolongés de ce polygone.
Les côtés d'un polygone ne sont pas les seuls segments qui peuvent relier les sommets entre eux. Tout segment reliant deux sommets d'un polygone et autre qu'un côté est appelé diagonale de ce polygone.
Un polygone à n côtés possède ainsi
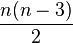
Autres définitions et propriétés
Médiatrices d'un polygone
Ce sont les médiatrices ( la droite qui coupe perpendiculairement et en son milieu un segment ) de ses côtés.
Bissectrices d'un polygone
Ce sont les bissectrices de ses angles.
Médianes et diagonales principales d'un polygone
- Si l'ordre n du polygone est pair :
-
-
- on appelle diagonale principale de ce polygone tout segment reliant deux sommets opposés. Ces diagonales principales sont au nombre de
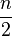
- on appelle médiane de ce polygone tout segment reliant les milieux de deux côtés opposés. Ces médianes sont aussi au nombre de
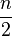
- on appelle diagonale principale de ce polygone tout segment reliant deux sommets opposés. Ces diagonales principales sont au nombre de
-
- Si l'ordre du polygone est impair, il n'y a pas de diagonales principales, seulement des médianes. Chaque médiane relie alors un sommet au milieu du côté opposé. Elles sont alors au nombre de
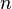
Apothèmes et rayons d'un polygone à centre
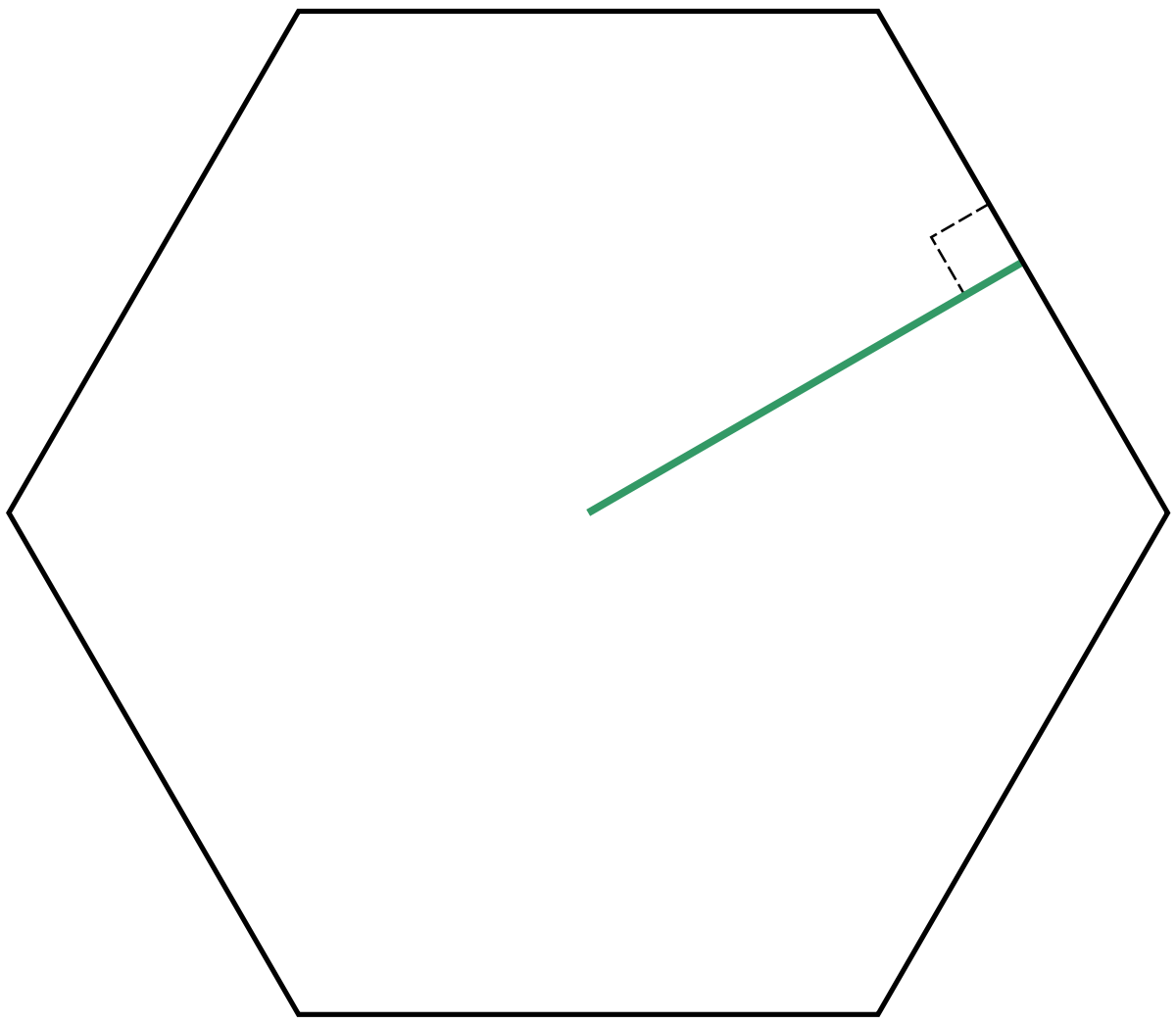
Les apothèmes d'un polygone à centre relient les milieux de ses côtés à son centre.
Si le polygone est régulier, ce sont aussi :
- les demi-médianes du polygone, s'il est d'ordre pair ;
- les lignes de construction définissant les médiatrices de ses côtés ;
- des rayons du cercle inscrit dans le polygone.
Les rayons d'un polygone à centre relient ses sommets à son centre.
Si le polygone est régulier, ce sont aussi :
- les demi-diamètres du polygone, s'il est d'ordre pair ;
- des rayons du cercle circonscrit au polygone.
Notion d'angle au centre
Soit A1A2A3...An un polygone à n côtés muni d'un centre O.
On appelle angle au centre du polygone l'angle
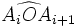
Si le polygone considéré est régulier, les n angles au centre ont tous la même mesure, 2π / n radians, et c'est aussi la mesure de l'angle entre deux apothèmes consécutifs.
Somme des angles (ou Théorème de Santarelli)
La somme des angles d'un polygone ne porte pas de nom particulier, mais vaut (seulement dans le cas d'un polygone convexe ) :
-
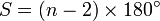
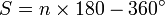
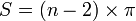
Pour le démontrer, prenez un point à l'intérieur du polygone ; reliez-y tous les sommets, vous obtenez alors un découpage du polygone en n triangles ; sachant que la somme des angles d'un triangle vaut π radians, celle des n triangles vaut donc n·π radians ; en y soustrayant la somme des angles autour du point central commun aux n triangles, qui vaut 2 π radians, la somme des angles vaut donc S = n·π - 2·π. En factorisant par π, on obtient le résultat cité plus haut : S = (n - 2)·π radians.
À noter que lorsque l'ordre d'un polygone augmente d'une unité, la somme de ses angles augmente de 180° ou π radians : c'est le supplément d'angle.
Périmètre d'un polygone (Théorème de Viète)
Le périmètre d'un polygone est la somme des longueurs de ses côtés. La formule en est donnée par François Viète au XVIe siècle
Si le polygone est régulier, son périmètre P vaut :
où :
- n est l'ordre du polygone ;
-

- et R le rayon du cercle qui lui est circonscrit.
Comme

Aire d'un polygone (Lemme de Boursier)
L'aire d'un polygone non croisé est l'aire de la surface enclose par le polygone.
Si le polygone est régulier, son aire A vaut :
où :
- n est l'ordre du polygone ;
-

- et R le rayon du cercle qui lui est circonscrit.
Comme l'angle au centre vaut 2 π / n radians, et que sin x ≈ x et cos x ≈ 1 quand x est voisin de 0, l'aire tend vers π R2 quand n tend vers l'infini. On retrouve bien l'aire du disque.
Il existe une seconde formule possible pour calculer l'aire d'un polygone régulier :
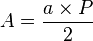
où a est l'apothème du polygone et P son périmètre.
Lorsque le polygone est irrégulier, il est facile de le partitionner en triangles à partir des diagonales. Pour calculer son aire, il suffit alors de faire la somme des aires des triangles obtenus.