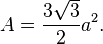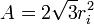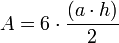Hexagone - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
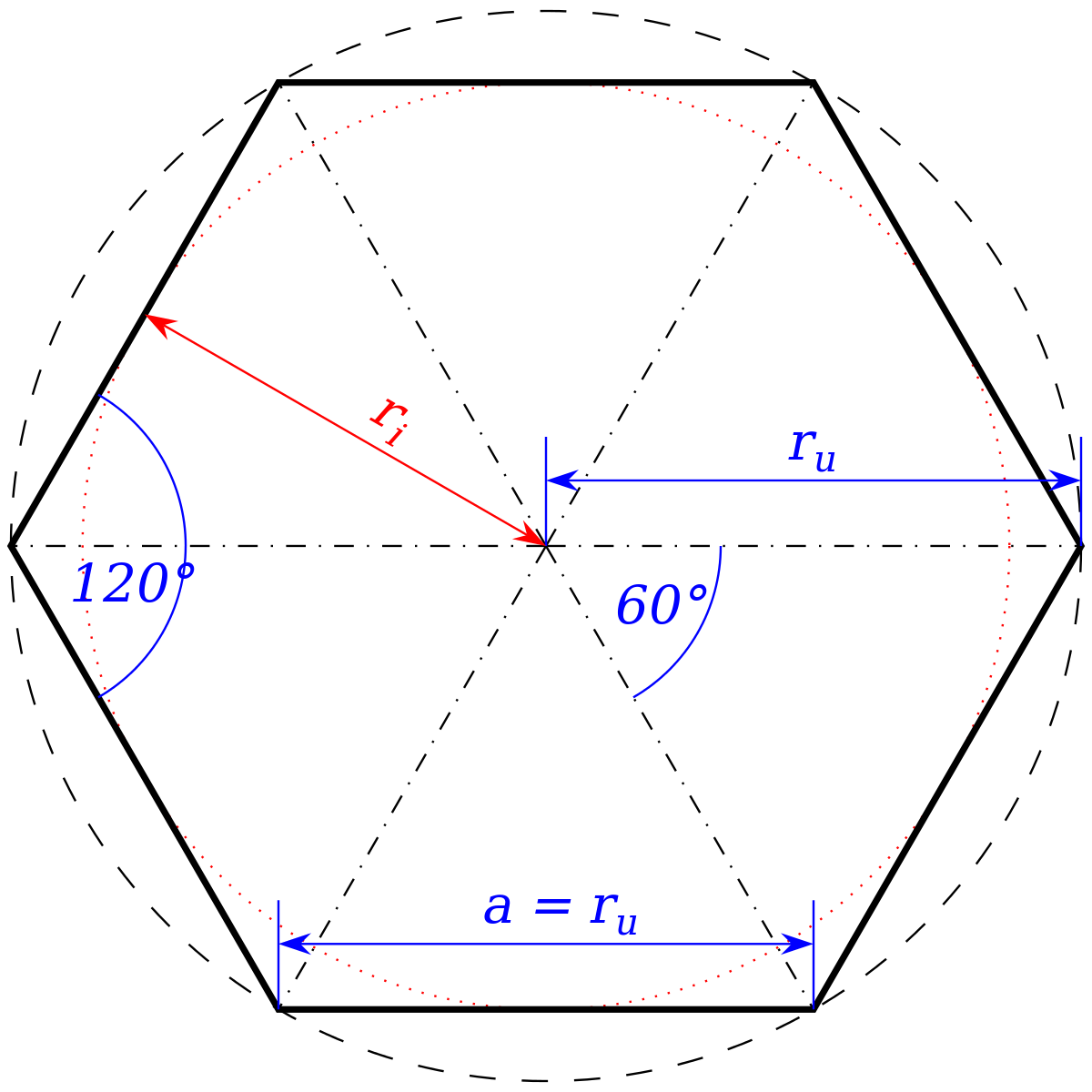
Un hexagone (du grec hexi = six et gonia = angle) est un polygone à six sommets et six côtés. Les angles internes d'un hexagone régulier sont tous de 120° et ses côtés sont de même mesure. Les hexagones réguliers peuvent se juxtaposer les uns les autres sans laisser aucune lacune, comme les carrés et les triangles équilatéraux, et sont ainsi utiles pour construire des pavages. Les cellules des rayons dans une ruche d'abeilles à miel sont hexagonales pour cette raison et parce que cette forme permet une utilisation efficace de l'espace et des matériaux de construction.
Calcul de la surface
La surface d'un hexagone régulier de côté
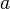
La surface d'un hexagone régulier dont le rayon du cercle inscrit est
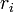
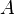
Propriétés générales
 | ||
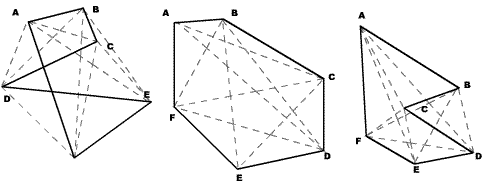| Hexagone croisé | Hexagone convexe | Hexagone concave |
| Sommets | Côtés | Diagonales |
| 6 | 6 | 9 |
Calcul de la surface par décomposition en triangles
La surface d'un hexagone régulier isométrique peut aussi se calculer avec la formule suivante :
Déduit de la formule générale du calcul de l'aire d'un polygone régulier possédant
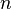
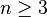
Cette formule permet de calculer l'aire en divisant l'hexagone en 6 triangles équilatéraux. Comme r = a, l'apothème
-
-
-
-
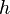
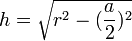
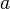
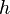
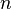
Autres
De par sa forme grossièrement hexagonale, la France métropolitaine est souvent appelée "Hexagone".
Hexagone régulier
Un hexagone régulier est un hexagone convexe inscrit dans un cercle et dont tous les côtés ont la même longueur (et les angles la même mesure).
Symétrie
Hexagone et triangle équilatéral
Construction d'un hexagone régulier
Un hexagone régulier est constructible car il vérifie le théorème de Gauss-Wantzel: 6 est le produit de 2 (en effet, 2 est puissance de 2) et de 3 (3 est un nombre de Fermat).
Il est possible de construire un hexagone régulier avec un compas et une règle, en suivant la méthode des éléments d'Euclide, qui consiste à construire 6 triangles équilatéraux:
 |  |
Pavages
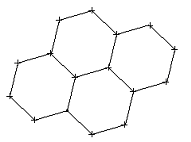
L'hexagone permet de créer un pavage périodique.
Dans la nature
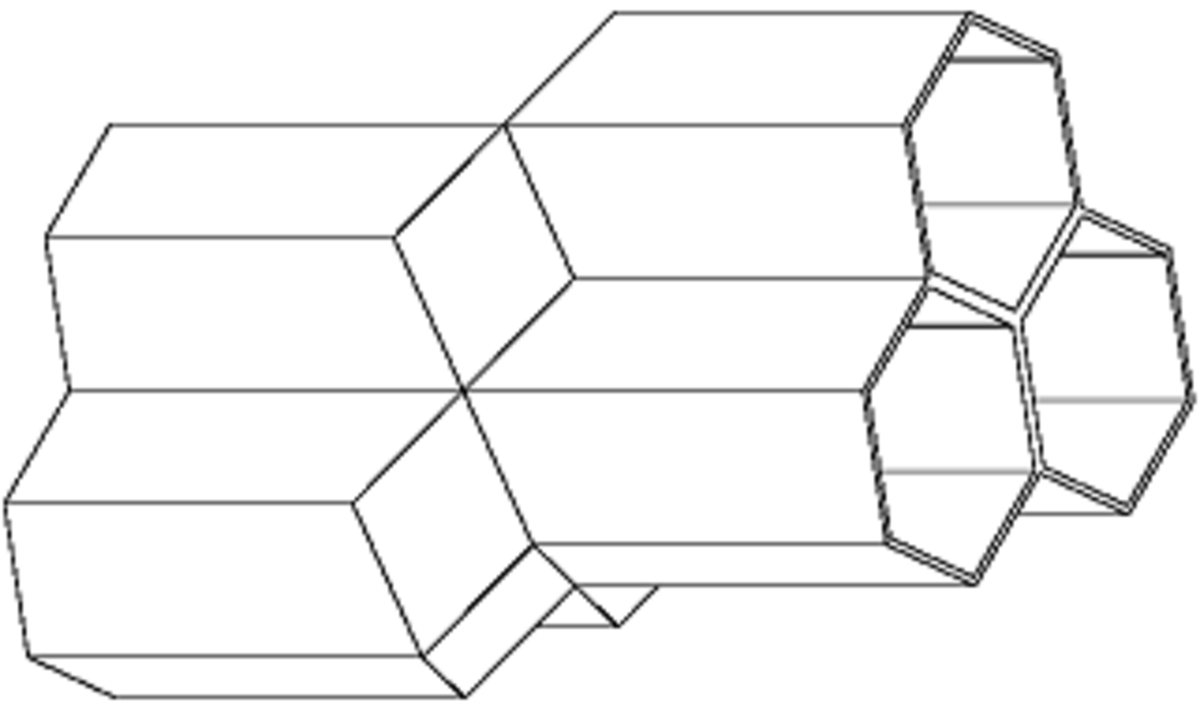
Les alvéoles d'abeille, construits afin de stocker le miel et le pollen ou les œufs et les larves, sont des prismes juxtaposés d’axes horizontaux qui constituent le gâteau de cire. Ce gâteau de cire est ainsi formé de deux séries d’alvéoles hexagonaux se rejoignant en leur base. L'hexagone est une figure optimale, pour l'abeille. Non seulement elle permet de paver le plan, mais, de plus, elle correspond à un optimum isopérimétrique, c'est-à-dire que parmi les figures régulières qui permettent de paver l'espace, l'hexagone correspond à la plus grande surface possible pour un périmètre donné. Aucune autre figure, permettant de paver l'espace n'utilise moins de cire que celle adoptée par les abeilles. Cette remarque est initialement l'œuvre de Pappus, un géomètre grec de l'antiquité.
Usages
Ballon de football aux couleurs du Brésil. Normalisée, la forme d'un ballon de football est composée de 20 faces hexagonales et 12 pentagonales. |
Hexagramme
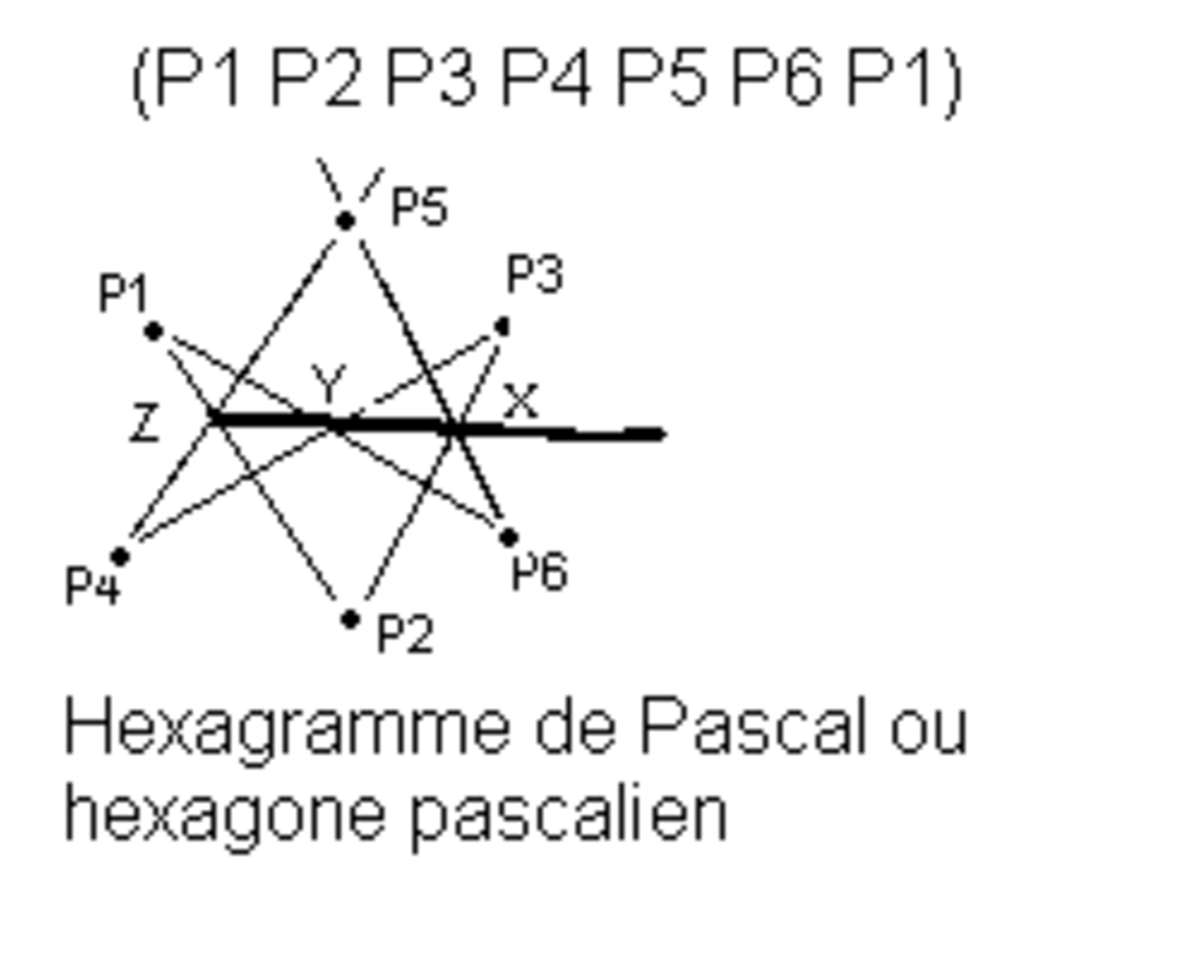
L’hexagramme de Pascal
Un hexagramme de Pascal est un hexagone irrégulier très particulier. Il est tel que les côtés opposés se coupent en trois points alignés. Cette configuration, inventée par Blaise Pascal, est très utile pour l'étude des ellipses, hyperboles, paraboles, cercles.
