Cycles (Géométrie algébrique) - Définition
La liste des auteurs de cet article est disponible ici.
Fonctorialité
Soit
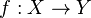
- f * [Z] = [k(ξ):k(f(ξ)][f(Z)] si l'extension k(ξ) / k(f(ξ)) est finie, et f * [Z] = 0 sinon.
Ce induit un homomorphisme de groupes
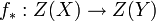
Degré d'un 0-cycle
On suppose que X est une variété algébrique sur un corps k (i.e. c'est un k-schéma de type fini). Pour tout point fermé x (donc 0-cycle irréductible), le corps résiduel k(x) est une extension finie de k. Si
| Z = | ∑ | ni[xi] |
| i |
est un 0-cycle, on définit son degré par
| degZ = | ∑ | ni[kxi):k]. |
| i |
C'est un entier qui dépend du corps de base k. L'application degré est un homomorphisme
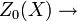
Théorème — Soit X une variété algébrique propre (par exemple projectif) sur un corps k. Soit Z un 0-cycle principal. Alors il est de degré 0.
Cela veut dire que dans le cas des variétés algébriques propres, l'application degré induit un homomorphisme de groupes
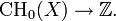
- Corollaire. Soit X une courbe projective sur un corps, alors l'application degré induit un homomorphisme de groupes de CH1(X) = CH0(X) dans
Références bibliographiques
William Fulton: Intersection Theory, second edition. - Springer Verlag, 1998
Correspondance
A écrire...

















































