Cycles (Géométrie algébrique) - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Définition - Diviseur principal et cycle principal - Exemples - Fonctorialité - Degré d'un 0-cycle - Références bibliographiques - Correspondance

Introduction

En géométrie algébrique, les cycles sont des combinaisons formelles de fermés irréductibles d'un schéma donné. Le quotient du groupe des cycles par une relation d'équivalence convenable aboutit aux groupes de Chow qui sont des objets fondamentaux.

Tous les schémas considérés ici seront supposés noethériens de dimension finie.

Définition

On fixe un schéma $X$ qu'on supposera noethérien de dimension finie $d$ . Pour tout entier positif ou nul $p$ , on appelle $p$ -cycle irréductible (resp. $p$ -cocycle irréductible) de $X$ un fermé irréductible de dimension $p$ (resp. codimension $p$ ). Un $p$ -cycle est une combinaison formelle finie

∑	n_i[Z_i]
i

où les coefficients $n i$ sont des entiers relatifs, et où les $Z i$ sont des $p$ -cycles irréductibles. On définit similairement les $p$ -cocycles. L'ensemble des $p$ -cycles est un groupe commutatif, qui est d'ailleurs le groupe abélien libre engendré par les fermés irréductibles de dimension $p$ de $X$ . On note ce groupe $Z p (X)$ . Similairement, le groupe des cocycles est noté $Z p (X)$ . On remarque que ces groupes sont nuls si $p > n$ .

Les 1-cocyles s'appellent les diviseurs de Weil. Ce sont donc des combinaisons entières de fermés irréductibles de codimension 1. Rappelons qu'un fermé irréductible est de codimension 1 si ce n'est pas une composante irréductible de $X$ , et si tout fermé irréductible qui le contient strictement est une composante irréductible de $X$ .

La somme directe (finie) des $Z p (X)$ est le groupe des cycles de $X$ .

Diviseur principal et cycle principal

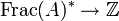
Soit $A$ un anneau local noethérien de dimension 1. Soit $f$ un élément régulier non-inversible de $A$ . On définit l'ordre de $f$ comme étant la longueur du $A$ -module artinien $A / f A$ . Notons-le $ord(f)$ . On montre que l'application ord est additif et induit donc un homomorphisme de groupes ${\rm Frac}(A)^* \to {\mathbb Z}$ où $Frac(A)$ désigne l'anneau total des fractions de $A$ . Noter que si $A$ est intègre, l'anneau total des fractions est simplement le corps des fractions.

Supposons $X$ intègre. Soit $f$ une fonction rationnelle non-nulle sur $X$ (c'est donc un élément du corps des fractions de $O X (U)$ pour tout ouvert $U$ ). Pour tout fermé irréductible $Z$ de codimension 1, de point générique $ξ$ , l'anneau local $O X,ξ$ est de dimension 1. On note $ord ξ (f)$ l'ordre de la fraction $f$ dans l'anneau local $O X,ξ$ . On pose

div(f) =	∑	ord_ξ(f)[Z_ξ]
	ξ

où la somme parcourt les points $ξ$ de codimension 1, et où par commodité dactylographique $Z ξ$ est l'adhérence de Zariski de ${ξ}$ (c'est un 1-cocycle irréductible). On montre aisément (parce que $X$ est noethérien) que c'est une somme finie. On a donc un diviseur de Weil. Un tel diviseur est appelé un diviseur principal sur $X$ . On a

$div(f g) = div(f) + div(f)$

et $div(1) = 0$ .

Par extension, les diviseurs principaux des fermés irréductibles de $X$ forment un sous-groupe de $Z (X)$ appelé le groupe des cycles principaux de $X$ . Par exemple si $X$ est de dimension 2, il y aura des diviseurs principaux de $X$ , mais aussi des 0-cycles qui sont principaux dans des fermés irréductibles de dimension 1 de $X$ .

On note $CH(X)$ le goupe quotient de $Z (X)$ par le sous-groupe des cycles principaux. Les images de $Z p (X)$ et de $Z p (X)$ dans $CH(X)$ sont notées $CH p (X)$ et $CH p (X)$ . Ce sont les groupes de Chow de $X$ .

On dira, même si cela comporte des pathologies en dehors des variétés algébriques intègres, que deux cycles sur $X$ sont rationnellement équivalents si leur différence appartient au groupe des cycles principaux.