Variété algébrique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Une variété algébrique est, de manière informelle, l'ensemble des racines communes d'un ensemble de polynômes en plusieurs indéterminées. C'est l'objet d'étude de la géométrie algébrique. Les schémas sont des généralisations des variétés algébriques.
Il y a deux points de vue (essentiellement équivalents) sur les variétés algébriques: elles peuvent être définies comme des schémas de type fini sur un corps (langage de Grothendieck), ou bien comme la restriction d'un tel schéma au sous-ensemble des points fermés. On utilise ici le deuxième point de vue, plus classique.
Définition
Une variété algébrique est, grossièrement, une réunion finie de variétés affines. Elle peut être vue comme un espace topologique muni de cartes locales qui sont des variétés affines, et dont les applications de transition sont des applications polynômiales.
Les points d'une variété algébrique sont localement des ensembles algébriques.
Variétés algébriques
On fixe un corps k. Un espace localement annelé (X,OX) en k-algèbres est constitué d'un espace topologique X et d'un faisceau de k-algèbres OX sur X tel que les germes OX,x aux points x de X sont des anneaux locaux
Une variété algébrique sur k est un espace localement annelé (X,OX) en k-algèbresqui admet un recouvrement fini par des ouverts affines Xi (c'est-à-dire que l'espace
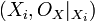
Bien que la structure d'une variété algébrique (X,OX) dépende du faisceau structural OX, notamment pour les variétés non réduites, on note généralement une variété algébrique simplement par X sans OX.
Si U est une partie ouverte de X, les éléments de l'anneau OX(U) s'appellent les fonctions régulières sur U. Dans des situations favorables, les fonctions régulières s'identifient à des applications de U dans k.
Exemples
- Les variétés affines sont par définition des variétés algébriques.
- Les variétés projectives sont des variétés algébriques. Une variété projective est affine si et seulement si elle est de dimension 0, c'est-à-dire consiste en un nombre fini de points.
- Soit X le plan affine Spmk[T,S], soit x0 = (0,0) le point de X correspondant à l'idéal maximal de k[T,S] engendré par T,S. Alors le complémentaire U de x0 est une partie ouverte. Une fonction régulière f sur U doit être régulière sur la partie ouverte
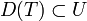
![f\in k[T,S]](https://static.techno-science.net/illustration/Definitions/autres/3/34d4f4e7ee3106b4fcaf69868c270221_9ab5df7db7ec848843f09d2e5a3f1b5c.png)
Fonctions régulières
Soit X une variété algébrique sur un corps algébriquement clos k. On fixe un ouvert U et une fonction régulière
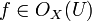
Pour tout
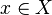
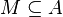
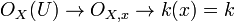
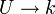
On suppose de plus que X est une variété réduite, c'est-à-dire que OX(U) est un anneau réduit pour tout ouvert U (cela revient à dire que X est une rénion finie d'ouverts affines SpmAi, avec les Ai réduits). Alors à l'aide du théorème des zéros de Hilbert, on montre sans peine que l'application
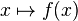
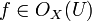
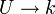
Morphismes
Un morphisme de variétés algébriques
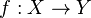
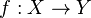
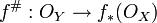
On peut expliciter le morphisme
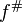
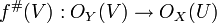
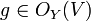
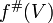
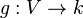
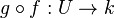
En général on omet
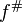
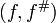
Étant données deux morphismes de variétés algébriques
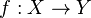
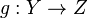
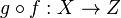
Le morphisme identité sur X est constitué de l'application identité
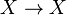
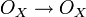
Un isomorphisme est un morphisme
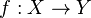
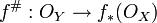
La classe des variétés algébriques sur k forment une catégorie.
- Morphismes vers une variété algébrique affine
Soit Y une variété algébrique affine associée à une k-algèbre A. Pour tout morphisme de variétés algébriques
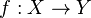
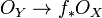
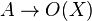
-
- Proposition L'application Mor
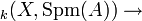
- Proposition L'application Mor
Restreinte aux variétés affines X, cette proposition dit que la catégorie des variétés algébriques affines sur k est équivalente à la catégorie (opposée) des algèbres de type fini sur k.

















































