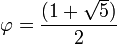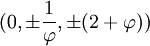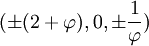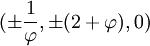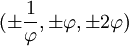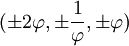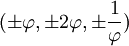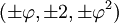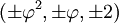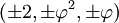Dodécaèdre tronqué - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Introduction
| Dodécaèdre tronqué | |
|---|---|
 | |
| | |
| Type | Solide d'Archimède |
| Faces | Triangles et décagones |
| Éléments : · Faces · Arêtes · Sommets · Caractéristique | 32 90 60 2 |
| Faces par sommet | 3 |
| Sommets par face | 3 et 10 |
| Isométries | |
| Dual | Triaki-icosaèdre |
| Propriétés | Semi-régulier et convexe, zonoèdre |
| modifier | |
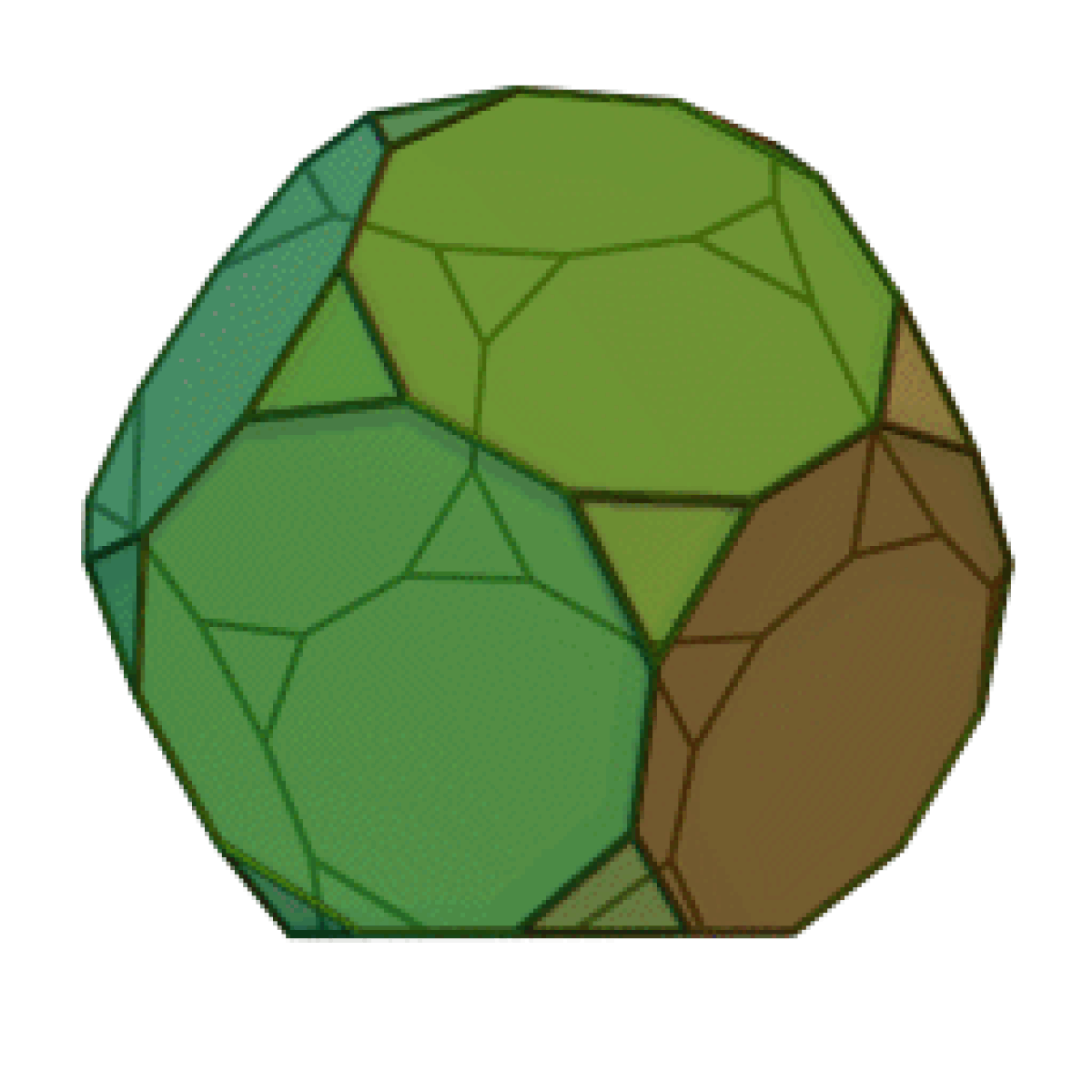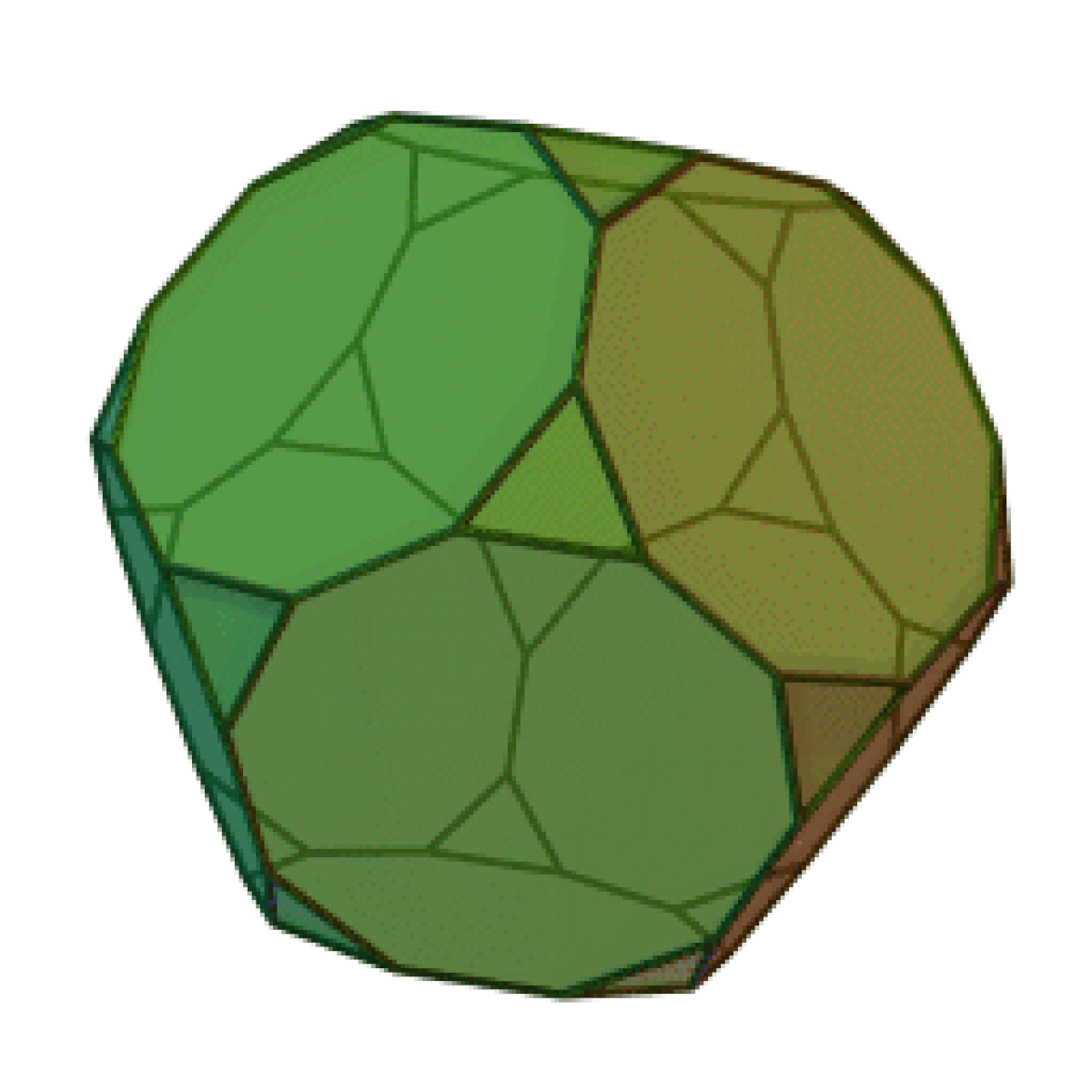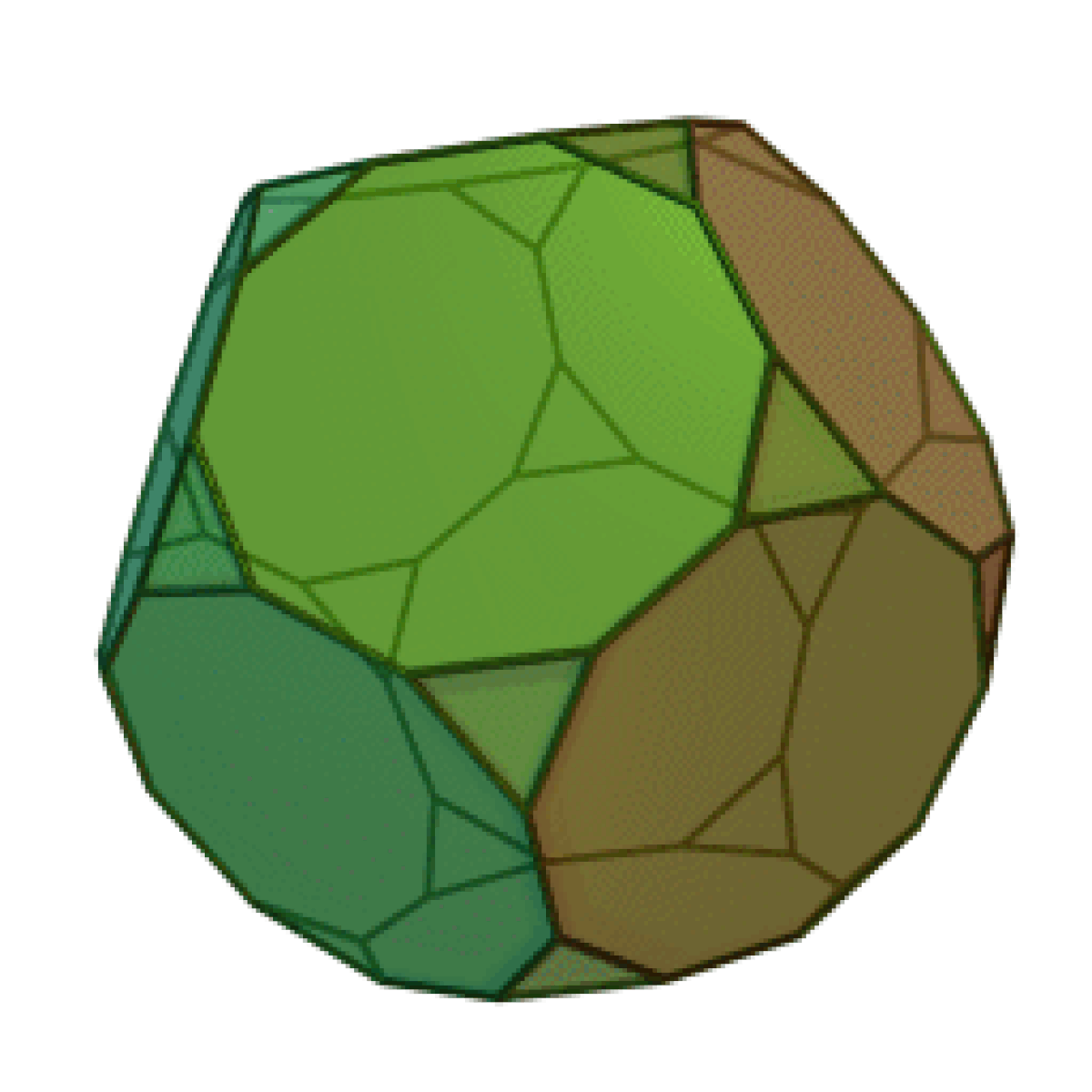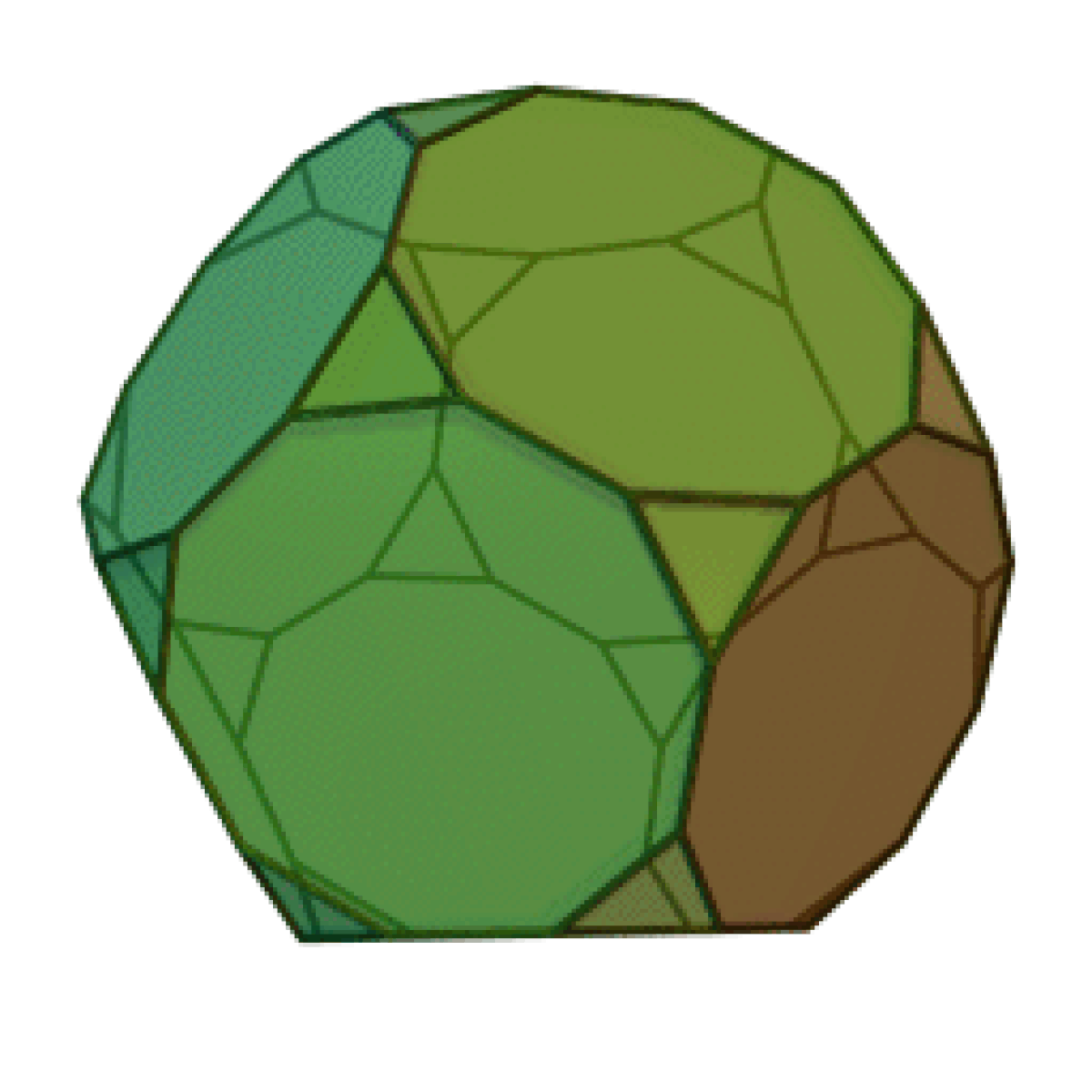
En géométrie, le dodécaèdre tronqué est un solide d'Archimède. Il possède 12 faces décagonales régulières, 20 faces triangulaires régulières, 60 sommets et 90 arêtes.
Relations géométriques
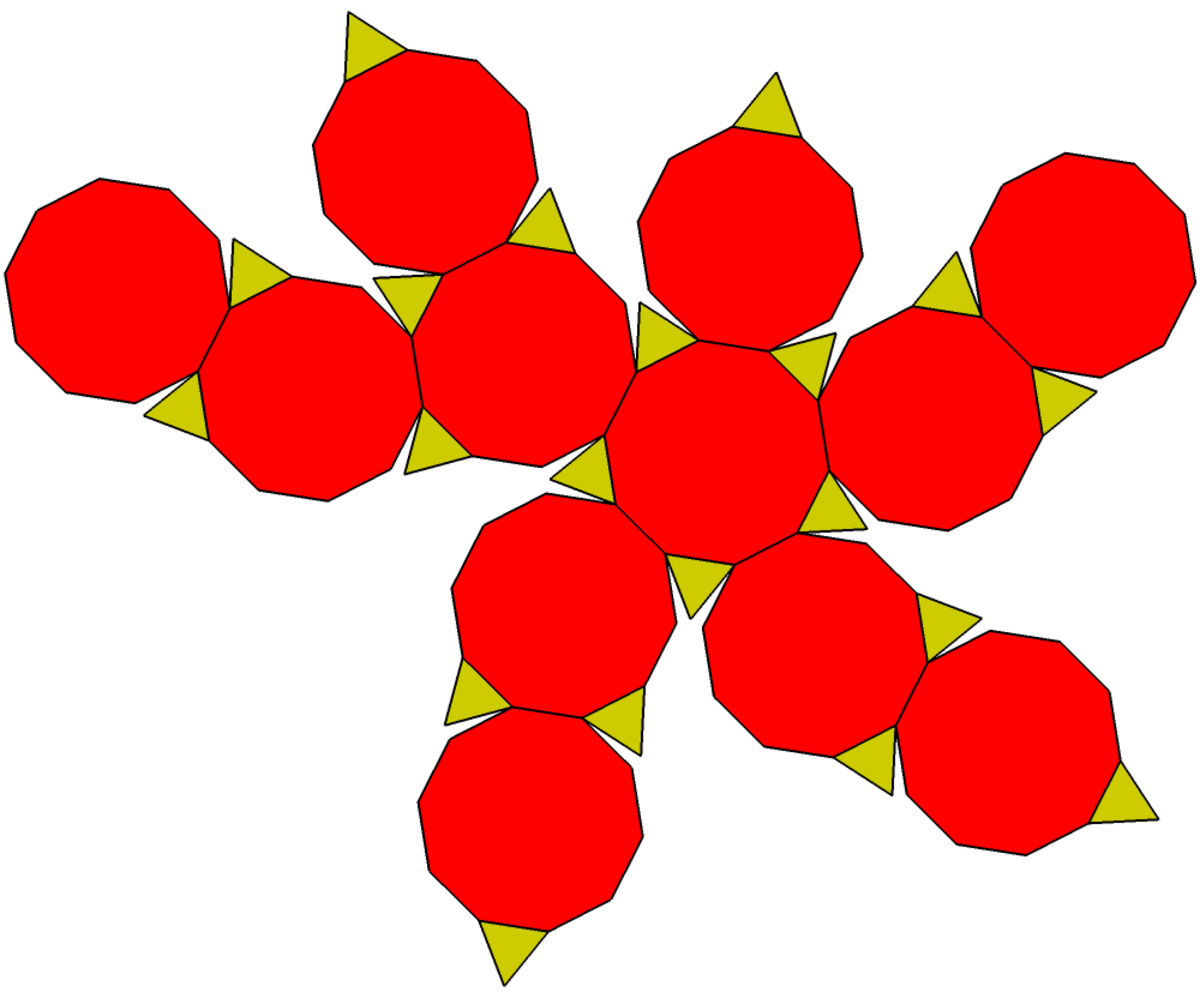
Ce polyèdre peut être formé à partir d'un dodécaèdre par troncature des coins, donc les faces pentagonales deviennent des décagones et les coins deviennent des triangles.
Coordonnées cartésiennes
Les coordonnées cartésiennes suivantes définissent les sommets d'un dodécaèdre tronqué centré à l'origine :
où