Polyèdre - Définition

Introduction

Un polyèdre est une forme géométrique à trois dimensions ayant des faces planes qui se rencontrent le long d'arêtes droites. Le mot polyèdre provient du grec classique πολυεδρον, à partir de poly-, racine de πολυς, "beaucoup" + -edron, forme de εδρον, "base", "siège" ou "face".

Historique

Les polyèdres ont été étudiés formellement par les anciens Grecs.

La définition ci-dessus peut sembler suffisamment claire pour la plupart d'entre nous, mais pas pour un mathématicien. Dans une remarque souvent citée mais rarement observée, Grünbaum (1994) nota que :

« Le Péché Originel dans la théorie des polyèdres remonte à Euclide, puis à travers Kepler, Poinsot, Cauchy et beaucoup d'autres... [en cela] qu'à chaque étape ... les auteurs ont échoué à définir ce que sont les 'polyèdres' ... »

Et depuis ce jour, il n'existe pas de définition universellement agréée sur ce qui fait que quelque chose est un polyèdre. La définition de polyèdre ne fait pas référence à la dimension de l'espace dans lequel il se trouve.

On peut néanmoins donner une définition utilisant le simplexe. Un polyèdre P de dimension p est la réunion d'un ensemble fini de simplexes S_i de dimension tel que chacune des d-faces () d'un simplexe S_i est un élément de P et tel que pour tout couple de simplexe S_i, S_j l'intersection est soit vide soit une (d-1)-face commune à S_i et S_j.

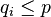
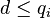
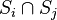
Ainsi un simplexe représente un cas particulier de polyèdre. Il est la réunion de ses d-faces et l'intersection de deux d-faces quelconques d'un simplexe est soit vide soit une face de dimension d − 1. Ainsi un triangle, qui est un 2-simplexe, est la réunion de segments et l'intersection de deux segments adjacents est un point qui est un sommet du triangle.

Nous pouvons au moins dire qu'un polyèdre est construit à partir de différentes sortes d'éléments ou d'entités, chacun associé avec un nombre différent de dimensions :

• 3 dimensions : le corps est limité par les faces, et correspond habituellement au volume compris à l'intérieur.
• 2 dimensions : une face est limité par un circuit d'arête, et est habituellement une région plane appelée un polygone. Les faces mises ensemble forment la surface polyédrique.
• 1 dimension : une arête joint un sommet à un autre et une face à une autre, et est habituellement une droite d'une certaine sorte. Les arêtes mises ensemble forment le squelette polyédrique.
• 0 dimension : un sommet est un point de coin.
• -1 dimension : la nullité est une sorte de non-entité requise par les théories abstraites.

Plus généralement en mathématiques et dans d'autres disciplines, le terme 'polyèdre' est utilisé pour faire référence à une variété de constructions reliées, certaines géométriques et d'autres purement algébriques ou abstraites.

En particulier, un polytope est un polyèdre convexe et borné.

Polyèdres traditionnels

Un polyèdre est traditionnellement une forme tridimensionnelle qui se compose d'un nombre fini de faces polygonales qui sont des parties de plans; les faces se rencontrent par paires le long des arêtes qui sont des segments de droite, et les arêtes se rencontrent aux points nommés sommets. Les cubes, les prismes et les pyramides sont des exemples de polyèdres. Le polyèdre entoure un volume limité dans l'espace à trois dimensions; quelquefois ce volume intérieur est considéré être une partie du polyèdre, quelquefois, seule la surface est considérée.

Les polyèdres traditionnels incluent les cinq polyèdres convexes réguliers que l'on nomme les solides de Platon : le tétraèdre (4 faces), le cube (ou hexaèdre) (6 faces), l'octaèdre (8 faces), le dodécaèdre (12 faces) et l'icosaèdre (20 faces). Les autres polyèdres traditionnels sont les quatre polyèdres non-convexes réguliers (les solides de Kepler-Poinsot), les treize solides d'Archimède convexes et les 53 polyèdres uniformes restants.

Plus petit polyèdre

Un polyèdre possède au moins 4 faces, 4 sommets et 6 arêtes. Le plus petit polyèdre est le tétraèdre.

Convexité, concavité

Un polyèdre est dit être convexe si sa frontière (incluant ses faces et ses arêtes) ne se coupe pas elle-même et si le segment joignant deux points quelconques du polyèdre fait partie de celui-ci ou de son intérieur. Autrement dit, un polyèdre est convexe si toutes ses diagonales sont entièrement contenues dans son intérieur. Il est possible de donner une définition barycentrique d'un tel polyèdre : Soit A₁, A₂, , A_n, n points non coplanaires ; le polyèdre convexe est l'ensemble des points M barycentres de : A₁, A₂, , A_n affectés de coefficients α₁, α₂, , α_n où chaque α_i est positif.

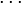
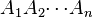
Les polyèdres symétriques

La plupart des polyèdres étudiés sont fortement symétriques. Il existe diverses classes de ces polyèdres :

• Sommet uniforme : si tous les sommets sont les mêmes, au sens où pour deux sommets quelconques, il existe une symétrie du polyèdre appliquant le premier isométriquement sur le deuxième.

• Arête uniforme : si toutes les arêtes sont les mêmes, au sens où pour deux arêtes quelconques, il existe une symétrie du polyèdre appliquant le premier isométriquement sur le deuxième.

• Face uniforme : si toutes les faces sont les mêmes, au sens où pour deux faces quelconques, il existe une symétrie du polyèdre appliquant le premier isométriquement sur le deuxième.

• Quasi-régulier : si le polyèdre est d'arête uniforme mais pas soit de face uniforme ou de sommet uniforme.

• Semi-régulier : si le polyèdre est de sommet uniforme mais pas de face uniforme et chaque face est un polygone régulier. (c'est une des nombreuses définitions du terme, dépendant de l'auteur, qui chevauchent la catégorie quasi-régulière).

Un polyèdre est semi-régulier si ses faces sont constituées de plusieurs sortes de polygones réguliers, et que tous ses sommets sont identiques. Ainsi sont par exemple les solides d'Archimède, les prismes et les antiprismes réguliers. La terminologie ne paraît pas tout à fait arrêtée. On parle parfois de solides semi-réguliers de la première espèce pour désigner ceux de ces solides qui sont convexes, et de solides uniformes pour le cas général. Les polyèdres de Catalan ne sont pas semi-réguliers, mais ont des faces identiques et des sommets réguliers. On dit parfois de tels polyèdres qu'ils sont semi-réguliers de la seconde espèce.

• Régulier : si le polyèdre est de sommet uniforme, d'arête uniforme et de face uniforme. (l'uniformité des sommets et l'uniformité des arêtes combinées implique que les faces sont régulières).

Partons d'un sommet et prenons les points situés à une distance donnée sur chacune des arêtes. Relions ces points, nous obtenons le polygone du sommet. Si celui-ci est régulier on dit que le sommet est régulier. Un polyèdre est régulier s'il est constitué de faces toutes identiques et régulières, et que tous ses sommets sont identiques. Ils sont au nombre de neuf, classiquement répartis en deux familles :

• les cinq solides de Platon : tétraèdre, cube, octaèdre, dodécaèdre et icosaèdre réguliers. Platon considérait ces solides comme l'image de la perfection. Les mathématiques modernes rattachent ces exemples à la notion de groupe.
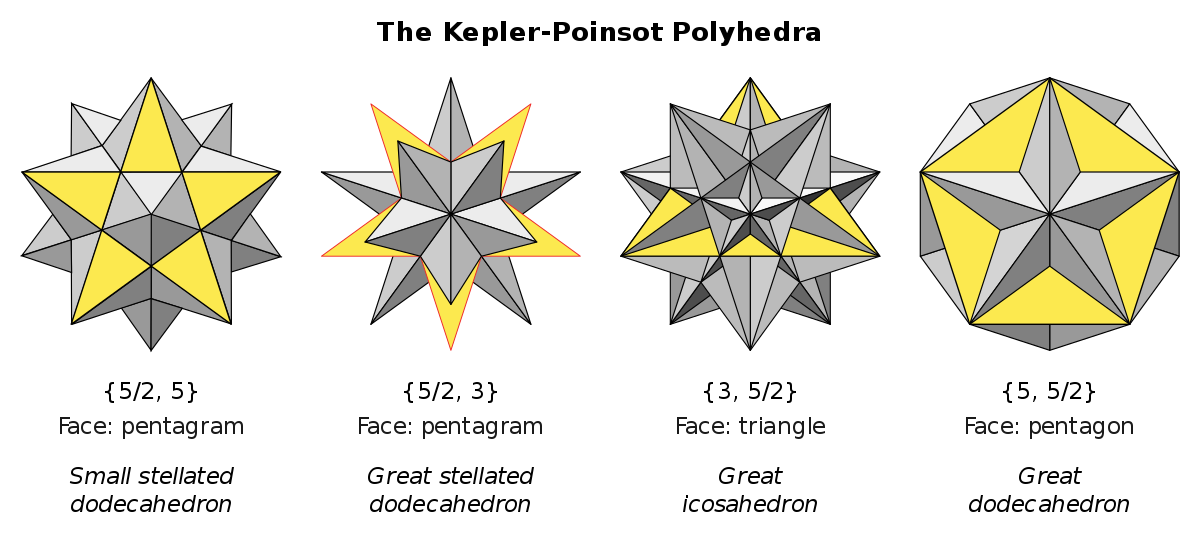
• les quatre polyèdres de Kepler-Poinsot, qui ne sont pas convexes.

• Uniforme : si le polyèdre est de sommet uniforme et chaque face est un polygone régulier, i.e. il est régulier ou semi-régulier.

On appelle solide uniforme un solide dont toutes les faces sont régulières et tous les sommets identiques. Ainsi sont donc tous les solides réguliers et semi-réguliers précédents. Ils sont en tout 75, auxquels il faut ajouter les deux familles infinies des prismes et des antiprismes.

Bien sûr, il est facile de tordre de tels polyèdres, de telle façon qu'ils ne sont plus symétriques. Mais, lorsqu'un nom de polyèdre est donné, tel que l'icosidodécaèdre, la géométrie la plus symétrique est toujours impliquée, sauf indication contraire.

Les groupes de symétrie polyédriques sont tous groupes de points et incluent :

• T - symétrie tétraédrique chirale ; le groupe de rotation pour un tétraèdre régulier; ordre 12.
• T_d - symétrie tétraédrique complète; le groupe de symétrie pour un tétraèdre régulier; ordre 24.
• T_h - symétrie pyritoédrique ; ordre 24. La symétrie d'un pyritoèdre [1].
• O - symétrie octaédrique chirale ; le groupe de rotation du cube et de l'octaèdre; ordre 24.
• O_h - symétrie octaédrique complète ; le groupe de symétrie du cube et de l'octaèdre; ordre 48.
• I - symétrie icosaédrique chirale ; le groupe de rotation de l'icosaèdre et du dodécaèdre; ordre 60.
• I_h - symétrie icosaédrique complète ; le groupe de symétrie de l'icosaèdre et du dodécaèdre; ordre 120.
• C_nv - symétrie pyramidale à n plis
• D_nh - symétrie prismatique à n plis
• D_nv - symétrie antiprismatique à n plis

Les polyèdres à symétrie chirale n'ont pas de symétrie axiale et par conséquent ont deux formes énantiomorphes qui sont les réflexions l'un de l'autre. Les polyèdres adoucis ont cette propriété.

Polyèdres réguliers

Un polyèdre régulier possède des faces régulières et des sommets réguliers. Le dual d'un polyèdre régulier est aussi régulier.

• Les polyèdres réguliers convexes sont aussi appelés les solides de Platon.

• Les polyèdres réguliers étoilés sont aussi appelés les polyèdres de Kepler-Poinsot.

Polyèdres quasi-réguliers et duaux

Les polyèdres quasi-réguliers sont à faces régulières, de sommet uniforme et d'arête uniforme. Il en existe deux convexes :

Les polyèdres duaux quasi-réguliers sont d'arête uniforme et de face uniforme. Il en existe deux convexes, en correspondance avec les deux précédents :

Les polyèdres semi-réguliers et leurs duaux

Le terme semi-régulier est diversement défini. Une définition consiste en "des polyèdres de sommet uniforme avec deux sortes ou plus de faces polygonales". Ils sont effectivement les polyèdres uniformes qui ne sont ni réguliers, ni quasi-réguliers.

Les polyèdres convexes et leurs duaux incluent les ensembles des :

	Uniforme convexe	Dual convexe	Uniforme étoilé	Dual étoilé
Régulier	Solides de Platon		Solides de Kepler-Poinsot
Quasi-régulier	Solides d'Archimède	Solides de Catalan	(pas de nom spécial)	(pas de nom spécial)
Semi-régulier			(pas de nom spécial)	(pas de nom spécial)
	Prismes	Diamants	Prismes étoilés	Diamants étoilés
	Antiprismes	Trapèzoèdres	Antiprismes étoilés	Trapèzoèdres étoilés

Il existe aussi beaucoup de polyèdres uniformes non-convexes, incluant des exemples de divers sortes de prismes.

Polyèdres nobles

Un polyèdre noble est à la fois isoèdrique (faces égales) et isogonal (de coins égaux). En plus des polyèdres réguliers, il existe beaucoup d'autres exemples.

Le dual d'un polyèdre noble est aussi un polyèdre noble.

Autres polyèdres à faces régulières

Faces égales régulières

Quelques familles de polyèdres, où chaque face est un polygone de même sorte :

• Les ont des triangles équilatéraux pour faces.

• En ce qui concerne les polyèdres dont les faces sont toutes des carrés : il n'existe que le cube, si les faces coplanaires ne sont pas permises, même si elles sont déconnectées. Autrement, il existe aussi le résultat du collage de six cubes sur les faces d'un seul, tous les sept de la même taille; il possède 30 faces carrées (comptant pour des faces déconnectées dans le même plan comme séparé). Ceci peut être étendu à une, deux ou trois directions : nous pouvons considérer l'union d'un grand nombre arbitraire de copies de ces structures, obtenues par translations de (exprimé en tailles de cubes) (2,0,0), (0,2,0), et/ou (0,0,2), par conséquent avec chaque paire adjacente ayant un cube en commun. Le résultat peut être un ensemble quelconque de cubes connectés avec les positions (a,b,c), avec les entiers a,b,c ou un au plus est pair.

• Il n'existe pas de nom particulier pour les polyèdres qui ont toutes les faces en forme de pentagones équilatéraux ou en pentagrammes. Il existe une infinité d'entre-eux, mais seulement un est convexe : le dodécaèdre. Le reste est assemblé par (collage) combinaisons de polyèdres réguliers décrit précédemment : le dodécaèdre, le petit dodécaèdre étoilé, le grand dodécaèdre étoilé et le grand icosaèdre.

Il n'existe pas de polyèdre dont les faces sont toutes identiques et qui sont des polygones réguliers avec six côtés ou plus car le point de rencontre de trois hexagones réguliers définit un plan. (voir polyèdre oblique infini pour les exceptions).

Deltaèdres

Un deltaèdre est un polyèdre dont les faces sont toutes des triangles équilatéraux. Il en existe une infinité, mais seuls huit sont convexes :

• 3 polyèdres réguliers convexes (3 des solides de Platon)
  • Tétraèdre
  • Octaèdre
  • Icosaèdre

• 5 polyèdre non-uniformes convexes (5 des solides de Johnson)
  • Diamant triangulaire
  • Diamant pentagonal
  • Disphénoïde adouci
  • Prisme triangulaire triaugmenté
  • Diamant carré gyroallongé

Les solides de Johnson

Norman Johnson a cherché les polyèdres non-uniformes ayant des faces régulières. En 1966, il publia une liste de 92 solides convexes, maintenant connue comme les solides de Johnson, et leur donna leurs noms et leurs nombres. Il ne prouva pas qu'ils n'étaient que 92, mais il conjectura qu'ils n'y en avait pas d'autres. Victor Zalgaller en 1969 démontra que la liste de Johnson était complète.

Les autres familles de polyèdres

Les pyramides

• Les pyramides sont auto-duales.

Les stellations et les facettages

La stellation d'un polyèdre est le processus d'expansion des faces (dans leurs plans), c’est-à-dire qu'elles se rencontrent pour former un nouveau polyèdre.

C'est la réciproque exacte du facettage qui est le processus d'enlèvement de parties d'un polyèdre sans créer de nouveau sommets quelconques. Le facettage permet d'obtenir, entre autres, de nombreux nouveaux solides semi-réguliers concaves. On construit de nouvelles faces régulières en regroupant les arêtes d'un polyèdre semi-régulier. Le plus simple est un héptaèdre construit à partir de l'octaèdre, constitué de trois faces carrées et de quatre faces triangulaires.

Troncatures

C'est l'opération qui consiste à raboter un sommet ou une arête. Elle conserve les symétries du solide.

Troncature des sommets

Cette opération permet d'obtenir sept des solides d'Archimède à partir des solides de Platon. On remarque en effet qu'en rabotant de plus en plus les arêtes d'un cube on obtient successivement le cube tronqué, le cuboctaèdre, l'octaèdre tronqué et enfin l'octaèdre. On peut aussi suivre cette série dans l'autre sens.

En partant du dodécaèdre on obtient le dodécaèdre tronqué, l'icosidodécaèdre, l'icosaèdre tronqué (qui donne sa forme au ballon de football), puis l'octaèdre.

Le tétraèdre donne le tétraèdre tronqué.

On peut appliquer cette opération au grand dodécaèdre ou au grand icosaèdre et obtenir des solides uniformes concaves.

Troncature des arêtes

À partir d'un cube, cette opération donne successivement un cuboctaèdre, puis un dodécaèdre rhombique.

À partir d'un dodécaèdre, on obtient l'icosidodécaèdre puis le triacontaèdre rhombique.

Les composés

Les composés polyèdriques sont formés comme des composés de deux polyèdres et plus.

Ces composés partagent souvent les mêmes sommets que les autres polyèdres et sont souvent formés par stellation. Certains sont listés dans la liste des modèles de polyèdre de Wenninger.

Les zonoèdres

Un zonoèdre est un polyèdre convexe où chaque face est un polygone avec une symétrie inverse ou, de manière équivalente, des rotations à 180°.