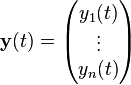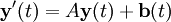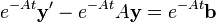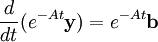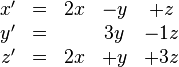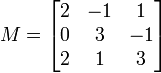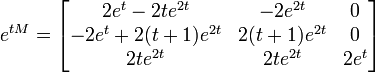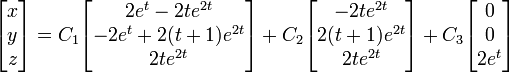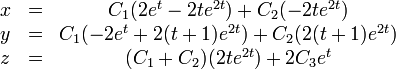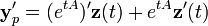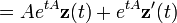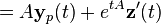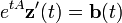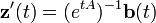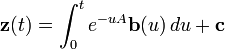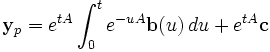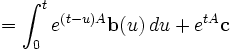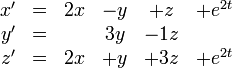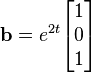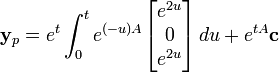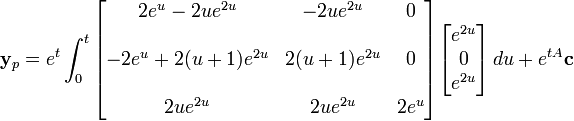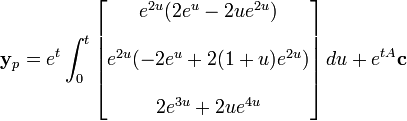Jeudi 1er Mai 2025
Rechercher 🔍

Exponentielle d'une matrice - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Définition - Calculs de l'exponentielle d'une matrice - Propriétés - Bibliographie - Applications

Bibliographie

  • Roger A. Horn et Charles R. Johnson, Topics in Matrix Analysis, Cambridge University Press, 1991. ISBN 0-521-46713-6.

Applications

Équations différentielles linéaires

L'exponentielle d'une matrice peut servir à résoudre des équations différentielles linéaires.

Sachant que y′ = Cy a pour solution eCt, considérons le vecteur

\mathbf{y}(t) = \begin{pmatrix} y_1(t) \\ \vdots \\y_n(t) \end{pmatrix}

Nous pouvons exprimer un système d'équations différentielles linéaires sous la forme

\mathbf{y}'(t) = A\mathbf{y}(t)+\mathbf{b}(t)

En multipliant par e−At, nous avons

e^{-At}\mathbf{y}'-e^{-At}A\mathbf{y} = e^{-At}\mathbf{b}
\frac{d}{dt} (e^{-At}\mathbf{y}) = e^{-At}\mathbf{b}

La résolution du système se ramène donc au calcul de eAt.

Exemple (équation homogène)

Supposons que nous ayons

\begin{matrix} x' &=& 2x&-y&+z \\ y' &=& &3y&-1z \\ z' &=& 2x&+y&+3z \end{matrix}

La matrice associée est

M=\begin{bmatrix} 2 & -1 & 1 \\ 0 & 3 & -1 \\ 2 & 1 & 3 \end{bmatrix}

et son exponentielle est

e^{tM}=\begin{bmatrix} 2e^t - 2te^{2t} & -2e^{2t} & 0 \\ -2e^t + 2(t+1)e^{2t} & 2(t+1)e^{2t} & 0 \\ 2te^{2t} & 2te^{2t} & 2e^t\end{bmatrix}

La solution générale du système est donc

\begin{bmatrix}x \\y \\ z\end{bmatrix}= C_1\begin{bmatrix}2e^t - 2te^{2t} \\-2e^t + 2(t+1)e^{2t}\\2te^{2t}\end{bmatrix} +C_2\begin{bmatrix}-2te^{2t}\\2(t+1)e^{2t}\\2te^{2t}\end{bmatrix} +C_3\begin{bmatrix}0\\0\\2e^t\end{bmatrix}

c'est-à-dire

\begin{matrix} x &=& C_1(2e^t - 2te^{2t}) + C_2(-2te^{2t})\\ y &=& C_1(-2e^t + 2(t+1)e^{2t})+C_2(2(t+1)e^{2t})\\ z &=& (C_1+C_2)(2te^{2t})+2C_3e^t\end{matrix}

Exemple (équation non-homogène, variation de la constante)

Pour une équation non-homogène, on peut utiliser une méthode semblable à la variation de la constante.

Nous cherchons une solution de la forme yp(t)=exp(tA)z(t) :

\mathbf{y}_p' = (e^{tA})'\mathbf{z}(t)+e^{tA}\mathbf{z}'(t)
= Ae^{tA}\mathbf{z}(t)+e^{tA}\mathbf{z}'(t)
= A\mathbf{y}_p(t)+e^{tA}\mathbf{z}'(t)

Avec yp comme solution :

e^{tA}\mathbf{z}'(t) = \mathbf{b}(t)
\mathbf{z}'(t) = (e^{tA})^{-1}\mathbf{b}(t)
\mathbf{z}(t) = \int_0^t e^{-uA}\mathbf{b}(u)\,du+\mathbf{c}

Alors,

\mathbf{y}_p = e^{tA}\int_0^t e^{-uA}\mathbf{b}(u)\,du+e^{tA}\mathbf{c}
= \int_0^t e^{(t-u)A}\mathbf{b}(u)\,du+e^{tA}\mathbf{c}

où c dépend des conditions initiales.

Exemple (non-homogène)

Supposons que nous ayons

\begin{matrix} x' &=& 2x&-y&+z&+e^{2t} \\ y' &=& &3y&-1z& \\ z' &=& 2x&+y&+3z&+e^{2t} \end{matrix}

Nous avons donc

M=\begin{bmatrix} 2 & -1 & 1 \\ 0 & 3 & -1 \\ 2 & 1 & 3 \end{bmatrix}

et

\mathbf{b}=e^{2t}\begin{bmatrix}1 \\0\\1\end{bmatrix}

Comme auparavant, la somme de la solution homogène et de la solution particulière donne la solution générale. La solution homogène étant connue, il suffit de trouver la solution particulière.

\mathbf{y}_p = e^{t}\int_0^t e^{(-u)A}\begin{bmatrix}e^{2u} \\0\\e^{2u}\end{bmatrix}\,du+e^{tA}\mathbf{c}
\mathbf{y}_p = e^{t}\int_0^t \begin{bmatrix} 2e^u - 2ue^{2u} & -2ue^{2u} & 0 \\ \\ -2e^u + 2(u+1)e^{2u} & 2(u+1)e^{2u} & 0 \\ \\ 2ue^{2u} & 2ue^{2u} & 2e^u\end{bmatrix}\begin{bmatrix}e^{2u} \\0\\e^{2u}\end{bmatrix}\,du+e^{tA}\mathbf{c}
\mathbf{y}_p = e^{t}\int_0^t \begin{bmatrix} e^{2u}( 2e^u - 2ue^{2u}) \\ \\ e^{2u}(-2e^u + 2(1 + u)e^{2u}) \\ \\ 2e^{3u} + 2ue^{4u}\end{bmatrix}\,du+e^{tA}\mathbf{c}
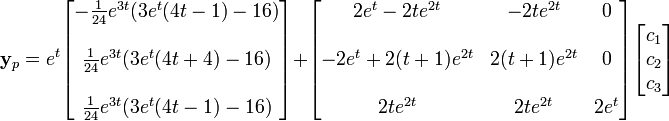
\mathbf{y}_p = e^{t}\begin{bmatrix} -{1 \over 24}e^{3t}(3e^t(4t-1)-16) \\ \\ {1 \over 24}e^{3t}(3e^t(4t+4)-16) \\ \\ {1 \over 24}e^{3t}(3e^t(4t-1)-16)\end{bmatrix}+ \begin{bmatrix} 2e^t - 2te^{2t} & -2te^{2t} & 0 \\ \\ -2e^t + 2(t+1)e^{2t} & 2(t+1)e^{2t} & 0 \\ \\ 2te^{2t} & 2te^{2t} & 2e^t\end{bmatrix}\begin{bmatrix}c_1 \\c_2 \\c_3\end{bmatrix} ,

expression qui peut être simplifiée pour obtenir la solution particulière cherchée.

Propriétés
- Introduction - Définition - Calculs de l'exponentielle d'une matrice - Propriétés - Bibliographie - Applications
miniature
Une éruption volcanique en 2018 responsable d'une explosion de vie 🌋
miniature
Un système d'exploitation pour les ordinateurs quantiques voit le jour 🖥️
miniature
Des singularités temporelles dans l'Univers ? 🕰️
miniature
Des fossiles de dinosaures mieux datés 🦖
miniature
Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭
miniature
Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆
miniature
Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜
miniature
Le rôle méconnu de la décharge dans l'usure des batteries 🔋
miniature
1
La fonte des glaces déplace les pôles: quelles conséquences ? 🌍
miniature
L'appareil photo de votre smartphone peut détecter l'antimatière 📱
miniature
Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐
miniature
Un mosasaure géant découvert dans le Mississippi 🦕
miniature
Problème, les galaxies meurent plus tôt que prévu 🌀
miniature
Ce lien entre cannabis et troubles psychotiques 🧠
miniature
Une révolution dans le refroidissement des puces électroniques ? 🔥
miniature
Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀
miniature
Lucy survole un astéroïde en forme de cacahuète 🚀
miniature
Découverte du fossile d'un dinosaure géant méconnu 🦕
miniature
Mars avait-elle un champ magnétique unilatéral ? 🔍
miniature
Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇
miniature
Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁
miniature
L'électroluminescence du graphène, une découverte inattendue ! 💡
miniature
Cet objet métallique n'a pas été fabriqué sur Terre 🔧
miniature
1
Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡
miniature
Cette super-Terre brûle les attentes des astronomes 🔥
miniature
Découverte exceptionnelle de fossiles d'amphibiens géants 🐸
miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
miniature
Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷
miniature
Des puces quantiques plus proches que jamais ⚡
miniature
1
Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬
miniature
En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊
Page générée en 0.103 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise