Vecteur - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, un vecteur est un élément d'un espace vectoriel, ce qui permet d'effectuer des opérations d'addition et de multiplication par un scalaire. Un n-uplet peut constituer un exemple de vecteur, à condition qu'il appartienne à un ensemble muni des opérations adéquates. On représente fréquemment les vecteurs comme de simples n-uplets ou, graphiquement, par des flèches. Les vecteurs sont des tenseurs d'ordre un. Les matrices sont des tenseurs d'ordre deux et les matrices d'une application linéaire transformant les vecteurs en forme linéaire constituent une forme particulière de vecteurs, appelées aussi bivecteurs.
En mathématiques, rigoureusement axiomatisée, la notion de vecteur est le fondement de la branche des mathématiques appelée algèbre linéaire.En algèbre multilinéaire, un champ vectoriel est une fonction de
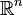
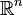
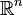
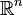
En physique, les vecteurs sont grandement utilisés,ils permettent de modéliser des grandeurs comme par exemple une force ou un champ électrique. On parle aussi de vecteur-vitesse.
La notion est issue de la combinaison des notions de couple de points de la géométrie euclidienne (qui permettent de définir les distance, mais aussi la direction et le sens), et des possibilités de calcul offertes par l'algèbre.
La notion de vecteur peut être définie en dimension deux (le plan), trois (l'espace euclidien usuel), et plus généralement des espaces de dimension quelconque.
Histoire
La notion de vecteur est le fruit d'une longue histoire, commencée voici plus de deux mille ans. Deux familles d'idées, d'abord distinctes, sont à l'origine de la formalisation. L'une d'elle est la géométrie, traitant de longueurs, d'angles et de mesures de surfaces et de volumes. L'autre correspond à l'algèbre, qui traite des nombres, de l'addition ou la multiplication et plus généralement d'ensembles munis d'opérations. Un vieux problème d'algèbre nous vient par exemple des Égyptiens et s'exprime de la manière suivante :
« On doit diviser 100 miches de pain entre dix hommes comprenant un navigateur, un contremaître et un gardien, tous trois recevant double part. Que faut-il donner à chacun ? »
Ces deux familles d'idées sont développées indépendamment, pour finir par converger vers la notion de vecteur.
Origines des deux concepts

La civilisation grecque développe la géométrie à un niveau inégalé à cette époque. L'un des fleurons est le traité nommé les Éléments d'Euclide, datant du IIIe siècle av. J.-C.. Il contient la formalisation, très rigoureuse pour l'époque, d'une géométrie, encore maintenant appelée euclidienne. On y trouve les définitions d'une droite, d'un plan ou de notre espace physique de dimension trois permettant de modéliser des volumes. Les propriétés des distances, des angles, des mesures de surfaces et de volumes sont étudiées. Les théorèmes fondateurs, comme ceux appelés Thalès ou Pythagore, sont explicités et démontrés.
L'algèbre y est peu développée et contient essentiellement de l'arithmétique. Les nombres entiers et rationnels sont étudiés ainsi que quelques irrationnels, c'est-à-dire les nombres qui ne s'écrivent pas sous forme d'une fraction d'entiers. Les nombres sont toujours strictement positifs.

La Chine développe les premières idées algébriques à l'origine des vecteurs. Un vieux texte, datant probablement du Ier siècle av. J.-C. : les Neuf Chapitres sur l'art mathématique y consacre sa huitième partie. Elle s'intitule Fang cheng ou Disposition rectangulaire et traite d'un problème maintenant appelé système d'équations linéaires. Cette culture n'en reste pas là, Qin Jiushao généralise cette étude à des nombres différents des entiers ou rationnels. Il utilise les congruences, inaugurant une démarche consistant à définir des vecteurs sur des ensembles de nombres exotiques. Il peut ainsi résoudre des problèmes liés au calendrier et aux alignements de planètes avec une très grande précision. La méthode utilisée ne sera connue qu'au XIXe siècle en Occident, sous le nom de pivot de Gauss. Ce résultat est suffisamment étonnant pour que Libbrecht précise que :
« Nous ne devrions pas sous-estimer la percée révolutionnaire de Qin, en effet, depuis le théorème des restes chinois de Sun Zi, on passe sans intermédiaire à un algorithme plus avancé que la méthode de Gauss elle-même, et il n'y a pas la moindre indication d'une évolution graduelle. »
L'aspect géométrique n'échappe pas aux mathématiciens chinois. Le dernier chapitre, le Gou gu comporte un équivalent du théorème de Thalès et de Pythagore.
Convergence de l'algèbre et de la géométrie
L'existence de lien entre ce que l'on appelle maintenant l'algèbre et la géométrie est ancienne. Les Babyloniens connaissaient déjà la propriété algébrique de la diagonale d'un carré de côté de longueur un, à savoir que son carré est égal à deux. Ils savaient de plus calculer cette valeur avec une remarquable précision. Ce lien est aussi connu des Grecs et des Chinois.
Il faut cependant attendre la civilisation arabe pour observer un progrès significatif. Leurs mathématiciens connaissaient les travaux des Grecs, particulièrement ceux d'Euclide. Les notations utilisées laissent penser qu'ils avaient aussi accès à des travaux des premiers mathématiciens chinois. Le progrès déterminant consiste à associer au plan géométrique des coordonnées. Omar Khayyam cherche les solutions d'un problème purement algébrique : trouver les racines d'un polynôme du troisième degré. Un système de coordonnées lui permet de visualiser ces racines comme les abscisses des intersections d'une parabole et d'une hyperbole.
Le système des coordonnées est repris en Europe. La volonté de maitriser la perspective pousse les peintres italiens à étudier les mathématiques. Filippo Brunelleschi découvre les lois de la perspective, issues d'une projection centrale. Ces résultats sont formalisés par Leon Battista Alberti . Les théoriciens de la perspective disposent de multiples talents. Ainsi Piero della Francesca , auteur d'un traité sur la question, est à la fois peintre et mathématicien. Giorgio Vasari indique, à propos de ses talents de géomètre « il ne fut inférieur à personne de son époque et peut-être de tout temps. ».
Apports de la physique
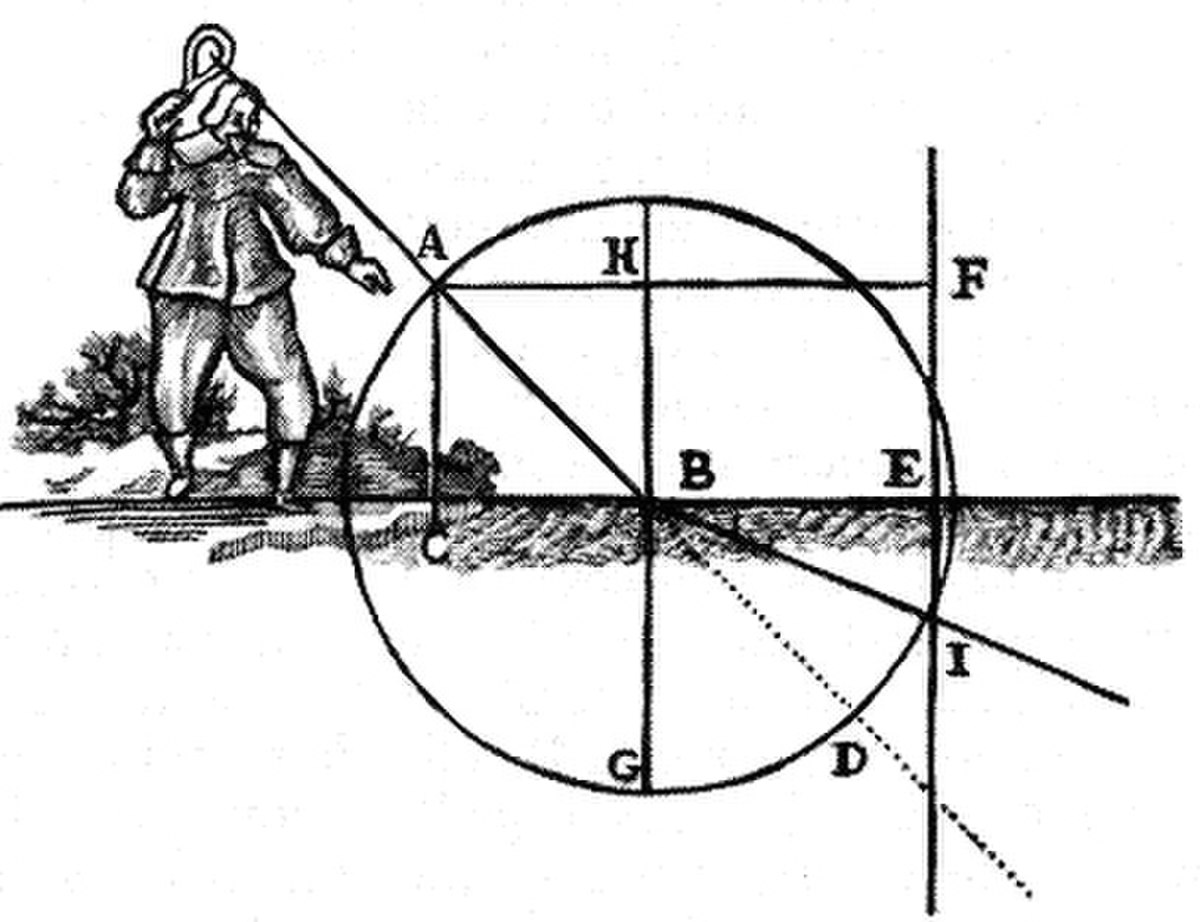
La physique est le moteur suivant de la convergence entre géométrie et algèbre. En 1604, Galileo Galilei établit la loi de la chute des corps. Les illustrations de ses notes montrent l'utilisation d'un repère. L'optique est la branche qui aboutit au progrès le plus marquant. Pierre de Fermat , qui connaissait les écrits de Galilée, et René Descartes s'écrivent des lettres au sujet de la dioptrique (la manière dont la lumière se réfléchit sur un miroir) et à la réfraction (la déviation d'un rayon lumineux quand il change de milieu, par exemple en passant de l'air à l'eau). Ils arrivent à la conclusion qu'un repère est une méthode systématique permettant d'appréhender tous les problèmes de géométrie euclidienne. Ces résultats sont consignés dans un traité de Descartes. Il écrit en introduction : « Comment le calcul d'arithmétique se rapporte aux opérations de géométrie ». Pour Descartes, calcul d'arithmétique signifie approximativement ce qui est maintenant appelé algèbre. Cette approche est particulièrement féconde pour l'étude d'une branche naissante des mathématiques : la géométrie analytique. Un exemple est donné par l'étude de la cycloïde. Cette courbe décrit la trajectoire d'un point de la surface d'une roue se déplaçant sans glissement sur un sol horizontal.
Isaac Newton développe la géométrie analytique et l'utilise en astronomie. Cette application est l'origine de l'utilisation du terme vecteur. En 1704, un dictionnaire technique anglais indique :
« Une ligne dessinée depuis une planète, se déplaçant autour d'un centre ou du foyer d'une ellipse, jusqu'à ce centre ou ce foyer, est appelé Vecteur par quelques auteurs de la Nouvelle Astronomie, car cette ligne semble porter la planète autour du centre. »
Ce terme apparait en français sous la plume de Pierre-Simon Laplace dans l'expression rayon vecteur, encore dans un contexte astronomique. Il vient du latin vector et désigne le conducteur d’un chariot. Son origine est plus ancienne, elle provient de l'indo-européen *VAG, ou *VAGH et signifie chariot.
Ainsi, au XVIIe siècle, le contexte géométrique et algébrique du vecteur est présent. En revanche, aucune formalisation n'est proposée et le terme, s'il est utilisé, désigne encore une grandeur scalaire.
Formalisations

La première formalisation des vecteurs est le fruit d'un travail de plusieurs mathématiciens durant la première moitié du XIXe siècle. Bernard Bolzano (1781 - 1848) publie un livre élémentaire contenant une construction axiomatique de la géométrie analogue à celle d'Euclide, fondée sur des points, droites et plans. Il adjoint les opérations algébriques d'addition et de multiplication. La géométrie projective, héritière du travail sur la perspective des peintres de la renaissance italienne, conduit Jean-Victor Poncelet (1788 - 1867) et Michel Chasles (1793 - 1880) à affiner les travaux de Bolzano. August Ferdinand Möbius (1790 - 1868) apporte sa pierre à l'édifice en développant le système de coordonnées barycentriques. Enfin, la formalisation encore actuellement enseignée, à partir des notions de bipoint et d'équipollence, est l'œuvre de Giusto Bellavitis (1803 - 1880).
Une autre voie est explorée, purement algébrique. William Rowan Hamilton (1805 - 1865) remarque que les nombres complexes représentent un plan euclidien. Il passe dix ans de sa vie à chercher un équivalent en dimension trois, et finit par trouver le corps des quaternions, de dimension quatre en 1843. Il propose deux nouvelles définitions pour les mots « vecteur » et « scalaire ». Un vecteur est pour lui un élément d'un sous-ensemble des quarternions, de dimension trois. Il écrit :
« Un vecteur est donc… une sorte de triplet naturel (suggéré par la géométrie) : et en conséquence nous verrons que les quaternions offrent une représentation symbolique simple sous forme trinomiale (i.x + j.y + k.z); ce qui ramène la conception et l'expression d'un tel vecteur à la forme la plus proche possible de celle obtenue avec les coordonnées cartésiennes et rectangulaires. »
Cette deuxième voie, qui donne pour la première fois une signification analogue aux formalisations modernes de la notion de vecteur, est ensuite précisée et enrichie. Elle consiste maintenant à définir un vecteur comme un élément d'un espace vectoriel.