Fonction de transfert - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Une fonction de transfert est une représentation mathématique de la relation entre l'entrée et la sortie d'un système linéaire invariant. Elle est utilisée dans l'analyse des systèmes continus (monovariables et multivariables), en traitement du signal, en théorie des communications, en électronique, en automatique et pratiquement dans toutes les techniques qui transforment une fonction du temps (ou, exceptionnellement, d'une autre variable) en une autre.
Dans le domaine temporel, un tel système est caractérisé par une réponse impulsionnelle. La transformation du signal d’entrée x(t) en signal de sortie y(t) s’effectue alors par une opération mathématique appelée convolution du signal d‘entrée et de la réponse impulsionnelle. Certaines transformations permettent de remplacer cette opération par un produit de la transformée X du signal d’entrée par la transformée H de la réponse impulsionnelle, appelée ‘’’fonction de transfert’’’, pour obtenir la transformée Y du signal de sortie.
Pour un signal continu, la fonction de transfert calculée en utilisant la transformation de Laplace donne des informations générales sur le système, en particulier sur sa stabilité.
La transformation de Fourier donne une information plus précise sur la réponse du système à chaque fréquence (en Hertz) ou pulsation (en radians par seconde). Cette information a une signification concrète et elle permet de déterminer les caractéristiques de la réponse à une excitation donnée beaucoup plus commodément qu’avec la réponse impulsionnelle.
À un signal discret est associée une fonction de transfert utilisant la transformation en Z.
Utilisation de la fonction de transfert en électronique
On utilise également cette fonction dans le domaine physique de l'électronique pour l'étude des amplificateurs opérationnels, sa définition cependant utilise des notations légèrement différentes :
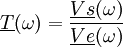
À partir de cette définition on peut trouver certaines propriétés du système étudié.
- Le module de la fonction de transfert nous donne le gain en fonction de la pulsation. On peut aussi étudier les limites du module dans les cas limites pour déterminer le comportement du système aux différentes pulsations.
C'est également ainsi que l'on détermine la pulsation de coupure, qui par définition est la pulsation telle que :
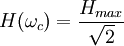
- L'argument de la fonction de transfert