Fréquence - Définition

Introduction

Ondes sinusoïdales de fréquences différentes : celle du bas a la plus haute fréquence et celle du haut, la plus basse.

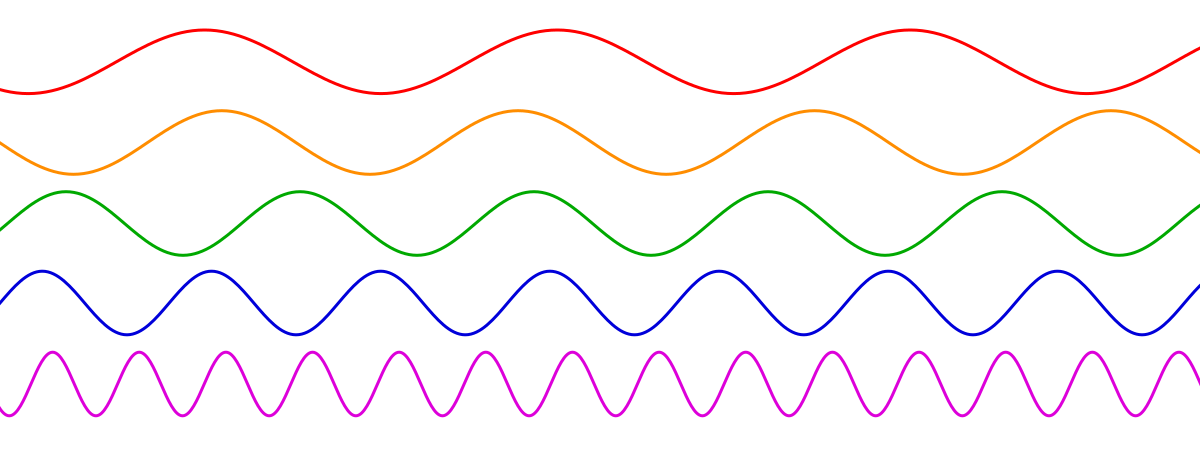
En physique, la fréquence désigne en général la mesure du nombre de fois qu'un phénomène périodique se reproduit par unité de temps. Ainsi lorsqu'on emploie le mot fréquence sans précision, on sous-entend la plupart du temps une fréquence temporelle. Par extension le terme est également utilisé lorsqu'un phénomène est périodique dans l'espace : on parle alors de fréquence spatiale.

Fréquence temporelle

Définition

La fréquence temporelle, ou momentanée, est notée généralement f ou ν et se définit comme l'inverse de la période temporelle notée T, soit . La période temporelle étant le temps nécessaire pour que le phénomène se reproduise identique à lui-même, la fréquence temporelle est donc pour une unité de temps donnée le nombre de fois que le phénomène se reproduit identique à lui-même.

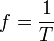
Si l'unité de temps choisie est la seconde (unité de temps dans le système international d'unités dit SI), la fréquence est alors mesurée en hertz dont le symbole est Hz (unité SI). Plus la valeur en hertz est élevée et plus la durée en seconde est courte.

Par exemple, pour une ondulation sur l'eau (des vagues), on peut mesurer la période temporelle T en se plaçant en un point (à la surface de l'eau) et en mesurant le temps que mettent deux hauteurs ou deux creux de vagues successifs pour se succéder en ce point. Ce temps donne la période et en prenant son inverse on obtient la fréquence de l'ondulation.

Il est possible d'utiliser d'autres relations pour définir la fréquence temporelle : ainsi pour un phénomène se propageant dans l'espace (par exemple l'amplitude d'une onde propagative), sa fréquence associée peut être également calculée par la relation où est la fréquence de l'onde (en Hertz), la célérité de l'onde (en mètres par seconde) et , la longueur d'onde (en mètres). Ainsi la fréquence représente le nombre de fois qu'une grandeur associée à un phénomène physique revienne identique à elle même après que le phénomène ait parcouru une certaine distance λ. Cette relation est valide, et équivalente à la première relation, seulement dans le cas d'un phénomène qui se propage spatialement (exclu le cas de l'onde stationnaire).

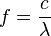
Par exemple, lorsqu'une onde progresse (comme des vagues sur l'eau), on peut identifier la longueur d'onde des vagues comme la distance entre deux hauteurs ou deux creux de vagues. La fréquence de l'ondulation est alors cette distance que multiplie la vitesse des vagues. Cela donne exactement le même résultat que pour l'exemple précédent où l'on mesure la période temporelle. À ce titre, la longueur d'onde λ est parfois appelée période spatiale par similitude avec la période temporelle T.

La fréquence f est reliée à la notion de pulsation, généralement notée ω, par la relation ω = 2πf. Dans le cas d'une rotation, 2π est la valeur en radian pour faire un tour complet : la pulsation est donc, dans ce cas, l'angle total en radion qu'effectue le système sur lui-même par unité de temps.

En physique

Dans le domaine de la physique ondulatoire on parlera d'une fréquence :

• d'oscillation mécanique (ressort, corde vibrante, vibration du réseau cristallin, vibration de molécules, etc...),
• d'oscillation acoustique dans le domaine audible (sonore) ou inaudible (infrasons, ultrasons, hypersons ...)
• d'oscillation électromagnétique (lumière visible, infrarouge, ultraviolet, etc...).

La fréquence est également utilisée pour quantifier la vitesse de fonctionnement d'un microprocesseur (voir Fréquence du processeur). Dans ce cas, la fréquence permet de connaître le nombre d'opérations par seconde que peut effectuer le composant (exemple : un processeur d'horloge 2Ghz peut traiter 2 000 000 000 d'opérations élémentaires par seconde).

En musique

En musique, la fréquence est reliée à la hauteur des sons entendus. La fréquence est exprimée en Hz, comme ci-dessus. Le spectre de fréquence entendu par l'oreille humaine s'étend environ de 20 à 20 000 Hz. La fréquence du «la» 440 a été établie comme fréquence de référence.

Mathématiquement, il est possible de faire plusieurs calculs entre les notes musicales et leurs fréquences. Une fréquence doublée donne une octave, tandis qu'une fréquence additionnée de son octave inférieure donne une quinte. Ensuite, l'addition d'une fréquence de 2 octaves inférieures donne une tierce. Par exemple :

En revanche, ces intervalles sont purs et non-tempérés; par conséquent, ils sonnent légèrement faux à une oreille conditionnée au tempérament égal.