Automatique - Définition
L'automatique fait partie des sciences de l'ingénieur. Cette discipline traite de la modélisation, de l'analyse, de la commande et, de la régulation des systèmes dynamiques. Elle a pour fondements théoriques les mathématiques, la théorie du signal et l'informatique théorique. L'automatique permet l'automatisation de tâches par des machines fonctionnant sans intervention humaine. On parle alors de système asservi ou régulé.
L'état désiré du système est nommé la consigne. Les hommes de l'art en automatique ou automatisme se nomment automaticiens.
Un exemple simple, est celui du régulateur de vitesse d'une automobile, il permet de maintenir le véhicule à une vitesse constante, vitesse-consigne prédéterminée par le conducteur.
Représentation graphique d'un système asservi
Les automaticiens ont l'habitude de représenter graphiquement un système asservi par l'utilisation de schéma-bloc.
Note : on parle généralement de procédé pour le système réel et de système pour désigner sa modélisation (généralement sous forme d'équations différentielles ou d'équations aux dérivées partielles). On parle également de système asservi pour désigner le système complet, avec le régulateur (correcteur).
Le schéma-bloc du système peut être composé :
- soit d'une seule entrée et d'une seule sortie (SISO : Single Input Single Output)
Exemple : la consigne de température d'un thermostat de chauffage domestique (l'entrée) et la température de la pièce (la sortie)
- soit de plusieurs entrées et plusieurs sorties (MIMO : Multiple Inputs Multiple Outputs)
Exemple : la consigne de température et de niveau d'un liquide dans une cuve industrielle (les entrées), la température et le niveau de ce liquide (les sorties)
Les entrées du système sont appelées variables exogènes, qui rassemblent les perturbations et les variables manipulées, commandes ou grandeurs réglantes. Elles sont souvent représentées de manière générique par la lettre u ou e. Les sorties du système sont appelées variables contrôlées, mesures ou grandeurs réglées. Elles sont souvent représentées de manière générique par la lettre y.
Les différents types de systèmes
- Systèmes à temps continus :
- Systèmes linéaires : utilise des fonctions de transfert issues de l'utilisation de la transformée de Laplace ou une représentation d'état linéaire continue, cette dernière représentation, sous forme d'équations différentielles ordinaires est plus riche et permet de conserver des propriétés telles que la commandabilité ou l'observabilité qui sont perdues par l'utilisation de la transformée de Laplace.
- Systèmes non-linéaires : utilise une représentation d'état non-linéaire continue
Il est à noter qu'aucun système n'est strictement linéaire, ne serait-ce que par les saturations (butées physiques, par exemple) qu'il comporte ou encore par les phénomènes d'hystérésis. Inversement, un système non-linéaire peut parfois être considéré comme linéaire dans une certaine plage d'utilisation. Il faut toujours garder à l'esprit que le système sur lequel on peut travailler n'est qu'un modèle mathématique de la réalité, et que par conséquent il y a une perte d'information lors du passage au modèle. Bien sûr, il incombe à l'ingénieur de juger la pertinence de son modèle vis à vis des objectifs fixés.
- Systèmes à temps discrets : ce sont des systèmes dont le temps à été discrétisé. Ces systèmes n'existent pas à l'état naturel (la majorité des systèmes physiques naturels sont de type à temps continu), mais étant donné que la plupart des contrôleurs utilisés en automatique sont calculés par des processeurs numériques, il est parfois intéressant de modéliser le système commandé comme un système à temps discret. La modélisation de ces systèmes utilise des fonctions de transfert avec la transformée en Z ou une représentation d'état discrète.
- Systèmes à évènements discrets : systèmes dont le fonctionnement peut être modélisé par des évènements discrets. Généralement, ces systèmes sont modélisés par des réseaux de Pétri, ou par les algèbres de dioïdes. Des exemples sont les réseaux ferroviaires, ou le fonctionnement d'une chaine de montage.
- Systèmes hybrides : Systèmes dont la modélisation nécessite l'utilisation des techniques liées aux systèmes continus et aux systèmes à évènements discrets, par exemple : une boite de vitesse de voiture.
Système bouclé
La technique d'automatisation la plus répandue est le contrôle en boucle fermée. Un système est dit en boucle fermée lorsque la sortie du procédé est prise en compte pour calculer l'entrée. Généralement le contrôleur effectue une action en fonction de l’erreur entre la mesure et la consigne désirée. Le schéma classique d'un système linéaire pourvu d'un régulateur linéaire en boucle fermée est le suivant:
La boucle ouverte du système est composée du procédé et du correcteur. La fonction de transfert de ce système en boucle ouverte est donc:
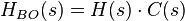
Avec cette architecture on peut recalculer une nouvelle fonction de transfert du système : la fonction de transfert en boucle fermée à l'aide des relations entre les différentes variables:
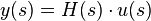
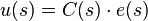
e(s) = r(s) − y(s)
On obtient alors :
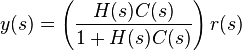
La fonction
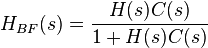
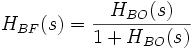
Remarques :
- La boucle de retour est le chemin qui part de la sortie et qui revient au comparateur avec le signe "moins". Dans cette boucle, il y a généralement un bloc représentant, dans la plus grande majorité des cas, un capteur. Si ce bloc a comme fonction de transfert "1" (ce qui équivaut à une abscence de bloc car la multiplication par 1 ne change rien), on dit que le schéma-bloc est à retour unitaire. La formule précédemment énoncée n'est valable que si le schéma-bloc est à retour unitaire.
- Quel que soit le schéma-bloc (unitaire ou non, avec ou sans perturbation, ...), le dénominateur de la fonction de transfert en boucle fermée est toujours : 1 + HBO(s) avec HBO(s) étant la fonction de transfert en boucle ouverte c'est-à-dire le produit de tous les blocs de la boucle, y compris ceux de la boucle de retour.
L'étude de cette fonction de transfert en boucle fermée permet l'analyse fréquentielle et temporelle du système général avec le contrôleur.
Stabilité
Dans le cas des systèmes linéaires représentés par une fonction de transfert, l'analyse des pôles permet de conclure sur la stabilité du système. On rappelle que les pôles d'une fonction de transfert sont les complexes p0,p1... qui annulent le dénominateur.
- Dans le cas d'une fonction de transfert continue utilisant la transformée de Laplace, tous les pôles doivent être à partie réelle strictement négative pour que le système soit stable.
- Dans le cas d'une fonction de transfert discrète utilisant la transformée en Z, tous les pôles doivent avoir un module inférieur à 1 pour que le système soit stable.
Attention, en automatique, le terme stabilité doit être défini précisément car il existe une dizaine de sortes de stabilités différentes. En général on fait référence à une stabilité asymptotique.
Dans le cas des systèmes non-linéraires, la stabilité est généralement étudiée à l'aide de la théorie de Lyapunov.
Les différentes techniques
Il existe différentes techniques pour synthétiser les régulateurs. La technique industrielle la plus largement utilisée est le régulateur PID qui calcule une action Proportionnelle, Intégrale et Dérivée en fonction de l’erreur consigne/mesure. Cette technique permet de satisfaire la régulation de plus de 90% des procédés industriels. Néanmoins, de nombreuses techniques de commandes dites " avancées " peuvent être utilisées pour la régulation de systèmes plus complexes lorsque le régulateur PID est insuffisant :
- La commande prédictive se basant sur l'utilisation d'un modèle dynamique du système pour anticiper son comportement futur.
- La commande robuste permettant de garantir la stabilité par rapport aux perturbations et aux erreurs de modèle.
- La commande adaptive qui effectue une identification en temps réel pour actualiser le modèle du système.
- La logique floue utilisant un réseau de neurones ou un système expert.
- Les contrôleurs non linéaires utilisant la théorie de Aleksandr Lyapunov, comme les commandes linéarisantes ou la commande par modes glissants, plus robuste.
- La commande par platitude différentielle, qui permet l'inversion de modèle sans passer par l'intégration des équations différentielles, et ainsi de calculer les signaux nécessaires sur les entrées pour garantir les trajectoires voulues en sortie.
Exemple de boucle de régulation
Reprenons l’exemple du moteur automobile.
On le commande en choisissant l'ouverture du papillon des gaz intégré au système d'injection du moteur. L'ouverture est directement liée à la force appliquée sur le piston donc à l’accélération du véhicule. Disons qu’elles sont proportionnelles (on néglige les pertes et la résistance de l’air sur le véhicule).
On veut maintenir une certaine vitesse, 90 km/h par exemple. 90 km/h est la consigne, il faut la comparer à la vitesse réelle donnée par un tachymètre.
La différence donne la variation de vitesse à réaliser. On en déduit l’accélération à demander au véhicule.
On obtient donc ce schéma.
En réalité, à cause des pertes, il faut maintenir une certaine accélération entre autres pour lutter contre la résistance de l’air.
Exemple d'automatisme industriel
La régulation industrielle est l'art de maintenir une grandeur physique, physico-chimique, ou chimique, appelée " mesure " égale à une grandeur cible appelée " consigne " quelles que soient les perturbations externes.
- Exemple : maintenir la température de sortie d'un four de raffinerie à 350°C quelle que soit la charge du four ou le pouvoir calorifique du combustible. La régulation industrielle se rencontre le plus souvent dans les procédés continus ou de production par lots (chimie, pétro-chimie, sidérurgie, pharmacie, agro-alimentaire, production d'énergie etc. )
- Le schéma illustre le fonctionnement d'un dispositif destiné à mettre en place une régulation industrielle.
Lexique
- Régulateur : un dispositif dont le but est d'agir sur le monde réel de manière à lui imposer un certain état.
- Grandeur réglée : C'est la grandeur mesurée dont on veut réguler la valeur.
- Mesure : La mesure est la grandeur physique, physico-chimique, ou chimique que doit atteindre le système à réguler. Elle s'exprime en unités physiques ( unités de pression, de niveau, de débit, de température, en unité de Ph, Rh, en unités de viscosité, densité etc. )
- Consigne : Elle s'exprime dans la même grandeur physique que la mesure. C'est la valeur " cible " que doit atteindre la mesure. Lors d'un changement de consigne, la boucle de régulation fonctionne en mode " asservissement ". Lorsque la boucle de régulation élimine les effets des perturbations, elle fonctionne en mode " régulation ".
- Organe correcteur : l'organe correcteur est le dispositif permettant de doser la grandeur réglante dans une boucle de régulation. Il peut être constitué soit d'une vanne automatique soit d'un variateur de vitesse associé à une pompe centrifuge ou à cylindrée variable soit d'un gradateur de puissance associé à des résistances chauffantes.
- Grandeur réglante : C'est la sortie du régulateur, soit la grandeur physique qui agit sur l'organe correcteur. Par exemple la puissance électrique délivrée dans des résistances chauffantes.
- Grandeur perturbatrice : Les grandeurs pertubatrices sont les grandeurs physiques qui peuvent s'opposer à l'action du régulateur mais que le régulateur ne contrôle pas. Il peut les mesurer directement ou indirectement pour apprécier leur action sur le système à réguler. Par exemple l'ouverture de la porte d'un four, la vitesse du vent pour le régulateur de direction d'un avion.
- Transmetteur de mesure : Un transmetteur de mesure est l'instrument qui traduit l'information d'un capteur pour la transformer en un signal transportable et utilisable par le système de régulation. Pour une température, on peut imaginer un capteur de type thermocouple dont la tension délivrée en micro-volts est transformée par un transmetteur en un signal 4-20 mA pour pouvoir être transporté sur quelques dizaines de mètres.
Bibliographie
- Patrick Prouvost, Automatique Contrôle et régulation, Dunod
- Sandrine Le Ballois, Pascal Codron : Automatique : systèmes linéaires et continus, Dunod
- Hassan K. Khalil, Non linear Systems, Prentice Hall
- Bode, Network analysis and feedback amplifier designer, D. Van Nostrand Company

















































