Fonctions d'Argyris - Définition
La liste des auteurs de cet article est disponible ici.
Matrice de passage
Remarque 5 : Cette construction n'est valable que pour le cas traité en exemple.
Pour trouver les fonctions de base d'Argyris dans un triangle donné, il faut multiplier le vecteur constitué des différentes fonctions dans le triangle de référence par une certaine matrice C que l'on explicitera ici.
Soient trois points non-alignés Xi = (xi,yi)(i = 1,2,3) qui formeront notre triangle T. Nous considérons la transformation affine FT qui envoie un point du triangle de référence
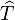
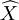
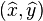
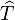
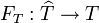
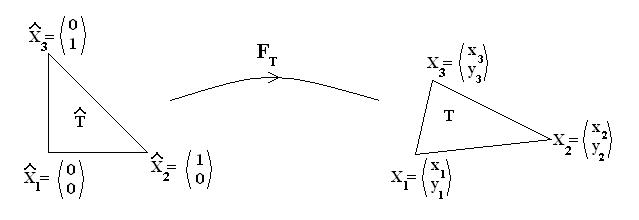
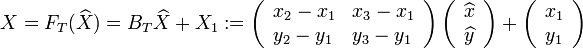
Afin de simplifier l'écriture, nous notons :
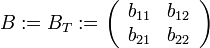
Notations
- Dans le reste de cette présentation, on utilisera des notations simplificatrices :
- Pour tout
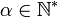
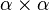
- Pour tout couple
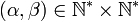
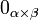
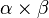
- Pour tout
- On note e1 (resp. e2 ; e3) l'arête ayant pour sommets les points X2 et X3 (resp. X3 et X1 ; X1 et X2). On note | ei | la longueur de l'arête ei,
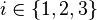
-
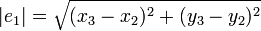
-
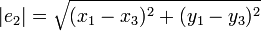
-
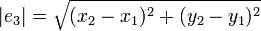
-
- Soit la matrice
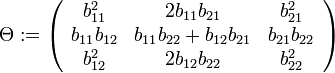
- Soit la matrice
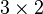
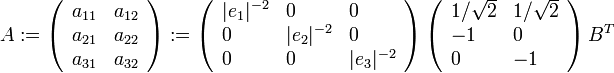
où
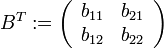
- Pour tout
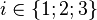
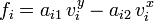
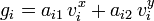
- Enfin, on note :
-
et
-
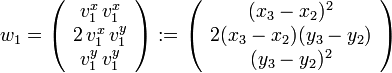
-
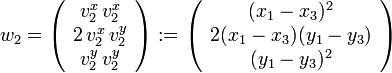
-
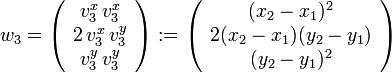
Remarque 6 : Si V est une vecteur ligne de taille n, on utilisera la notation VT pour l'écrire en tant que vecteur ligne de taille n : cela s'appelle la transposée du vecteur V (où encore le vecteur transposé de V). Exemple :
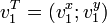
Construction de la matrice C
La matrice C se construit comme le produit de deux matrices C = D * E, où
- D est une matrice
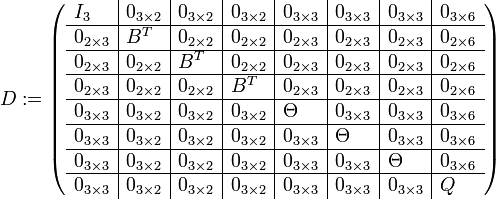
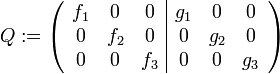
- E est une matrice
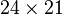
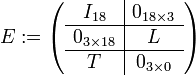
où
-
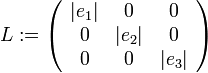
-
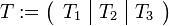
- T1 est une matrice
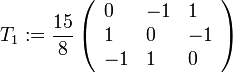
- T2 est une matrice
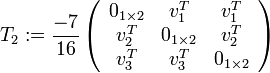
- T3 est une matrice
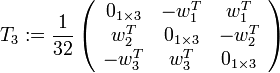
- T1 est une matrice
Exemple
Voici la liste des fonctions de base d'Argyris dans le triangle de référence avec la condition correspondante (cela signifie que le degré de liberté associé à la condition vaut 1 et que les autres valent 0).
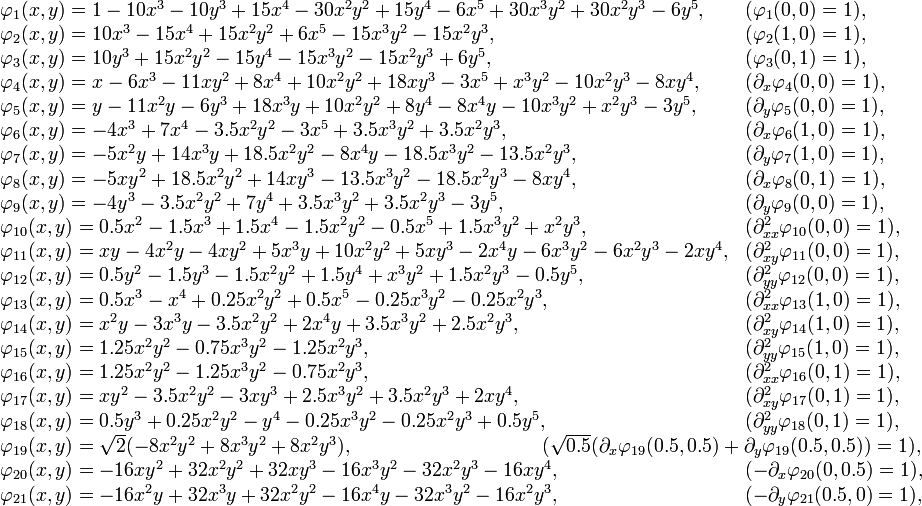
Remarque 4 : L’ordre n’a a priori aucune importance. Pour la programmation (ou l’utilisation de manière générale), il faut néanmoins se fixer un ordre et le conserver tout le temps.
Explications :
- La condition concernant la normale est
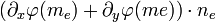
- Expliquons maintenant comment se forme la matrice A.
Tout d'abord, le vecteur colonne U est composé des coefficients à déterminer, c'est-à-dire
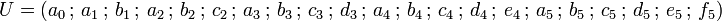
Voyons comment se compose, par exemple, les lignes 1 et 6 de la matrice liées aux conditions
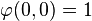
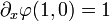
Donc la première ligne de la matrice M est (1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0).
-
![\left. \begin{array}{l} \varphi_6(x,y)=a_0+a_1x+b_1y+a_2 x^2+b_2 xy+c_2 y^2+a_3 x^3+b_3 x^2 y+c_3 x y^2+d_3 y^3+a_4x^4+b_4 x^3 y\\[4pt] \,\,\,\,\,\,\,\,+c_4 x^2 y^2+d_4 x y^3+e_4 y^4+a_5 x^5+b_5 x^4 y+c_5 x^3 y^2+d_5 x^2 y^3 + e_5 x y^4+f_5 y^5\\[6pt] \Rightarrow \partial_x \varphi_6(x,y)=a_1+2a_2 x+b_2 y+3a_3x^2+2b_3 xy+c_3y^2+4a_4x^3+3b_4x^2y+2c_4xy^2+d_4y^3\\[4pt] \,\,\,\,\,\,\,\,+5a_5x^4+4b_5x^3y+3c_5x^2y^2+2d_5xy^3+e_5y^4\\[6pt] \Rightarrow\partial_x \varphi_6(1,0)=a_1+2a_2+3a_3+4a_4+5a_5. \end{array}\right.](https://static.techno-science.net/illustration/Definitions/autres/8/8a34333661a383fb41890b4b69906bd2_9a63a9c0140714c35bc9cd9ff9774d37.png)
Donc la sixième ligne de la matrice M est (0,1,0,2,0,0,3,0,0,0,4,0,0,0,0,5,0,0,0,0,0).
Bibliographie
- V. Girault, P.-A. Raviart. Finite Element Methods for Navier-Stokes Equations. Theory and algorithms. Springer Series in Computational Mathematics, 5. Springer-Verlag, Berlin, 1986.
- S. Nicaise, K.Witowski and B. I. Wohlmuth. An a posteriori error estimator for the Lamé equation based on equilibrated fluxes. IMA Journal of Numerical Analysis, 28, no.2, pp 331-353, 2008.
- Librairie de getfem++
- V. Domínguez, F.J. Sayas. Algorithm 884: A simple MATLAB implementation of the Argyris element. ACM Trans. Math. Software 35, Article 16, 2008.
- M. Okabe. Full-explicit interpolation formulas for the Argyris triangle. Comput. Methods Appl. Mech. Engrg. 106, no. 3, pp 381--394, 1993.
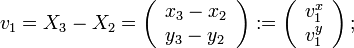
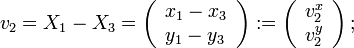
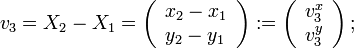
![\left. \begin{array}{l} \varphi_1(x,y)=a_0+a_1x+b_1y+a_2 x^2+b_2 xy+c_2 y^2+a_3 x^3+b_3 x^2 y+c_3 x y^2+d_3 y^3+a_4x^4+b_4 x^3 y\\[4pt] \,\,\,\,\,\,\,\,+c_4 x^2 y^2+d_4 x y^3+e_4 y^4+a_5 x^5+b_5 x^4 y+c_5 x^3 y^2+d_5 x^2 y^3 + e_5 x y^4+f_5 y^5\\[6pt] \Rightarrow \varphi_1(0,0)=a_0. \end{array} \right.](https://static.techno-science.net/illustration/Definitions/autres/f/f2835fd6b866c52f66bfa2a130a6d0a8_dc9eea9234d0e3c78f04b601bb7438ae.png)