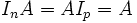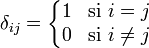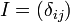Matrice identité - Définition
En algèbre linéaire, la matrice unité ou matrice identité (cette dernière dénomination étant un anglicisme) est une matrice carrée avec des 1 sur la diagonale et des 0 partout ailleurs. Nous pouvons l'écrire
Puisque les matrices peuvent être multipliées à la seule condition que leurs types soient compatibles, il y a des matrices unité de tout ordre. In, est la matrice unité d'ordre n est donc définie comme une matrice diagonale avec 1 sur chaque entrée de sa diagonale principale. Ainsi:
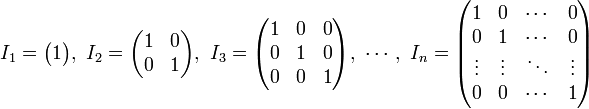
Concernant la multiplication des matrices, les matrices unités vérifient:
pour tous p, n entiers naturels non nuls et pour toute matrice A à n lignes et p colonnes,
Ce qui montre que la multiplication par une matrice unité n'a aucun effet sur une matrice donnée.
En particulier si n=p, In est l'élément neutre pour la multiplication des matrices carrées d'ordre n.
Il est possible aussi de noter les coefficients de la matrice unité d'ordre n avec le symbole de Kronecker ; le coefficient de la i-ème ligne et j-ème colonne s'écrit :
et donc la matrice unité I est égale à
Si l'ordre n'est pas précisé, ou qu'il est trivialement déterminé par le contexte, nous pouvons la noter simplement I.