Fonctions d'Argyris - Définition

Introduction

Les fonctions d’Argyris (ou éléments d’Argyris) est un outil en méthodes des éléments finis. Elles sont utilisées pour décrire un polynôme dans un triangle d’un maillage en employant seulement des données connues sur le bord du triangle (comme les valeurs au sommet, les valeurs des dérivées premières et secondes au sommet, ainsi que les valeurs « liées aux arêtes »). l'avantage est que l'on peut se ramener à un espace de dimension finie que l'on peut utilisé pour le calcul numérique.

Utilisées en modélisation numérique, ces fonctions furent introduites dans les années 1950; mais d'autres styles de fonctions sont également employées en pratique en fonction des problèmes à résoudre.

Introduction

Contexte

John Hadji Argyris (1913-2004) est l’un des précurseurs dans le domaine des méthodes des éléments finis, utilisée lors de résolution numérique d’équations différentielles issues de la physique, mécanique… comme la théorie des plaques. Ses concepts sont apparus en premier lors de la Seconde Guerre Mondiale, ce qui rendait ses premiers résultats top secret.

Le principe des fonctions d'Argyris consiste à exprimer un polynôme avec pour seules informations des données relatives au maillage du domaine. Bien évidemment, d'autres fonctions sont utilisées en Méthodes des Eléments Finis (Lagrange, Raviart-Thomas, Nédélec, GaussLobatto, Hermite, Morley, Bell…) ayant chacune leurs avantages ainsi que leurs inconvénients (tout dépend du problème que l'on veut résoudre).

Les éléments d'Argyris sont exclusivement dénommés ainsi pour la dimension 2 ( ). En dimension 1, voire 3, on parle plutôt d'éléments de type Argyris.

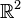
Cadre d’étude

On se place dans . Les variables sont appelées x et y. Soit T un triangle quelconque, non aplati.

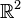
Les fonctions d'Argyris liées à T sont des fonctions de base de l'espace vectoriel qui représente l'ensemble des polynômes à deux variables x et y ( ) de degré au plus 5.

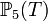
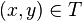
Approche formelle

Un élément s'écrit de manière unique sous la forme

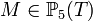
M = a₀ + a₁x + b₁y + a₂x² + b₂xy + c₂y² + a₃x³ + b₃x²y + c₃xy² + d₃y³ + a₄x⁴ + b₄x³y + c₄x²y² + d₄xy³ + e₄y⁴ + a₅x⁵ + b₅x⁴y + c₅x³y² + d₅x²y³ + e₅xy⁴ + f₅y⁵.

Ainsi, la seule donnée des coefficients suffit à écrire tout élément de . C'est pourquoi l'espace est un espace de dimension 21 (nombre de coefficients à déterminer).

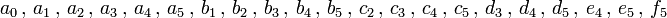
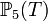
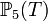
Il nous faut alors 21 relations (conditions) indépendantes afin de pouvoir déterminer ces 21 coefficients : on appelle cela les degrés de liberté.

Une base possible est {1,x,y,x²,xy,y²,x³,x²,y²,y³,x⁴,x³y,x²y²,xy³,y⁴,x⁵,x⁴y,x³y²,x²y³,xy⁴,y⁵}: on l'appelle la base canonique.

Dans la pratique, il est extrêmement difficile (et surtout pas pratique) de pouvoir trouver les 21 coefficients avec cette base. C'est pourquoi nous formulons une base différente formée des fonctions d'Argyris. Elles sont liées à des conditions données :

• sur la valeur de la fonction M en chaque sommet (3 relations);
• sur la valeur des dérivées premières de la fonction M en chaque sommet (6 relations);
• sur la valeur des dérivées secondes de la fonction M en chaque sommet (9 relations);
• sur la valeur "liée à la normale" pour chaque arête (3 relations).

Remarque 1 : Ces conditions ne sont pas uniques : on peut toujours trouver d'autres conditions, mais celles-ci sont les plus simples à mettre en application.

Remarque 2 : Le dernier point concerne la valeur "liée à la normale". C'est une définition un peu particulière qui peut être différente selon les travaux. Vous trouverez ici une définition possible et qui est la plus couramment utilisée.

Avec ces données, il est possible de calculer toutes les fonctions d'Argyris pour n'importe quel triangle : il suffit pour cela de résoudre un système linéaire AU=B où :

• A est une matrice 21*21;
• U est un vecteur de taille 21 composé des 21 coefficients;
• B est un vecteur de taille 21 dont toutes les composantes sont nulles sauf une qui correspond à la condition adéquate.

Vous pourrez trouver un exemple de fonctions d'Argyris dans la partie avec les conditions indiquées entre parenthèses.

Remarque 3 : Résoudre ce système est équivalent à inverser la matrice A.

En pratique, il est impensable de calculer toutes les fonctions de bases pour chaque triangle car le nombre de triangles peut être énorme (de l'ordre de plusieurs millions par exemple). C'est pourquoi, on calcule les fonctions sur un triangle particulier dit de référence ayant pour sommets les points (0;0), (1;0),(0;1) et on en "déduit" les fonctions d'Argyris dans un triangle particulier.