Diagonale - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Dans le plan
On appelle diagonale d'un polygone tout segment reliant deux sommets non consécutifs (non reliés par un côté). Un polygone à n côtés possède
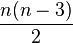
On appelle diagonale principale ou parfois diamètre d'un polygone tout segment reliant deux sommets opposés. Un polygone à n côtés possède
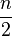
Dans l'espace
On appelle diagonale de l'espace une diagonale d'un polytope, diagonale de l'espace principale une diagonale principale d'un polytope, diagonale de l'espace brisée une diagonale brisée d'un hypercube.
On appelle triagonale une diagonale d'un polyèdre, triagonale principale une diagonale principale d'un polyèdre, triagonale brisée une diagonale brisée d'un cube.
On appelle quadragonale une diagonale d'un polytope à quatre dimensions, quadragonale principale une diagonale principale d'un polytope à quatre dimensions, quadragonale brisée une diagonale brisée d'un tesséract.
Dans les matrices
On appelle diagonale d'une grille ou matrice une rangée diagonale descendante reliant un bord à un autre. Voir aussi matrice diagonale.
On appelle antidiagonale d'une grille ou matrice une rangée diagonale ascendante reliant un bord à un autre.
On appelle aussi première diagonale l'unique diagonale descendante d'une matrice carrée et seconde diagonale l'unique diagonale ascendante d'une matrice carrée.
On appelle diagonale brisée d'une grille ou matrice toute paire de rangées parallèles à une diagonale principale et totalisant autant d'éléments que la plus petite dimension de la grille ou matrice.
On appelle diagonale dominante d'une matrice carrée la première diagonale lorsque celle-ci vérifie pour tout i : |
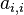
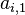
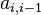
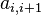
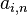
Propriétés liées
Un quadrilatère est un parallélogramme si, et seulement si, ses diagonales se croisent en leur milieu.

















































