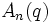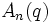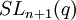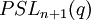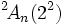Groupe de type de Lie - Définition

Lectures avancées

Une référence standard :

• Simple Groups of Lie Type par Roger W. Carter, ISBN 0-471-50683-4

Les groupes classiques sont décrits dans

• La géométrie des groupes classiques par Jean Dieudonné

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Group of Lie type »

Au sujet des notations

Malheureusement, il n'existe pas de notation standard pour les groupes de type de Lie finis, et la littérature contient des douzaines de systèmes de notations incompatibles et confus.

• Les groupes de type sont quelquefois notés (le groupe spécial linéaire projectif) ou .

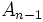
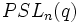
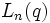
• Les groupes de type sont quelquefois notés (le groupe symplectique) ou (ce qui prête à confusion).

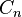
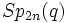
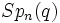
• La notation pour les groupes orthogonaux prête particulièrement à confusion. Certains symboles utilisés sont , , , , mais il existe tellement de conventions qu'il n'est pas possible, hors contexte, de dire exactement à quels groupes ils correspondent. En particulier certains auteurs désignent par un groupe qui n'est pas le groupe orthogonal, mais le groupe simple correspondant.

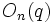
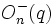
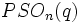
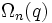
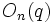
• Pour les groupes de Steinberg, certains auteurs écrivent (et ainsi de suite) pour le groupe que d'autres auteurs désignent par . Le problème est que deux corps interviennent, l'un d'ordre , et son corps fixe d'ordre q, et les avis divergent sur celui qui devrait être inclus dans la notation. La convention " " est plus logique et conforme, mais la convention " " est de loin la plus commune.

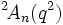
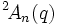
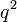
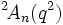
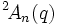
• Selon les auteurs, des groupes tels que sont les groupes de points à valeurs dans le groupe algébrique simple, ou simplement connexe. Par exemple, peut signifier soit le groupe spécial linéaire , soit le groupe projectif spécial linéaire . Donc peut désigner 4 groupes différents, selon l'auteur.