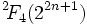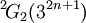Groupe de type de Lie - Définition

Les petits groupes de type de Lie

Beaucoup des plus petits groupes dans les familles ci-dessus ont des propriétés spéciales non partagées par la plupart des membres de la famille.

• Quelquefois les plus petits groupes sont résolubles plutôt que simples; par exemple les groupes SL₂(2) et SL₂(3) sont résolubles.

• Il existe beaucoup d'isomorphismes "accidentels" entre divers petits groupes de type de Lie (et les groupes alternés). Par exemple, les groupes SL₂(4), PSL₂(5) et le groupe alterné sur 5 points sont tous isomorphes.

• Certains des petits groupes ont un multiplicateur de Schur qui est plus grand que prévu. Par exemple, les groupes A_n(q) ont habituellement un multiplicateur de Schur d'ordre (n + 1, q - 1), mais le groupe A₂(4) possède un multiplicateur de Schur d'ordre 48, à la place de la valeur prévue 3.

Pour une liste complète de ces exceptions, voir la liste des groupes finis simples. Beaucoup de ces propriétés spéciales sont reliées à certains groupes sporadiques simples. L'existence de ces "petits" phénomènes n'est pas entièrement une question de "trivialité" ; ils se reflètent ailleurs, par exemple en théorie de l'homotopie.

Les groupes alternés se comportent quelquefois comme s'ils étaient des groupes de types de Lie sur un corps à 1 élément (mais un tel corps n'existe pas). Certains des petits groupes alternés ont aussi des propriétés exceptionnelles. Les groupes alternés ont habituellement un groupe d'automorphismes extérieurs d'ordre 2, mais le groupe alterné sur 6 points possède un groupe d'automorphismes extérieurs d'ordre 4. Les groupes alternés ont en général un multiplicateur de Schur d'ordre 2, mais ceux sur 6 ou 7 points ont un multiplicateur de Schur d'ordre 6.

Les groupes de Suzuki-Ree

Vers 1960, Michio Suzuki fit sensation en découvrant une nouvelle série infinie de groupes qui semblait, de prime abord, non relié aux groupes algébriques connus. Ree savait que le groupe algébrique possédait un automorphisme "supplémentaire" en caractéristique 2, dont le carré était l'automorphisme de Frobenius. Il trouva que si un corps fini de caractéristique 2 possède aussi un automorphisme dont le carré est l'application de Frobenius, alors un analogue de la construction de Steinberg donne les groupes de Suzuki. Les corps possédant un tel automorphisme sont ceux d'ordre , et les groupes correspondants sont les groupes de Suzuki

.

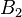
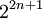
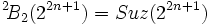
(à strictement parler, le groupe Suz(2) n'est pas compté comme un groupe de Suzuki car il n'est pas simple : c'est le groupe de Frobenius d'ordre 20). Ree réussit à trouver deux nouvelles familles similaires

et

de groupes simples en utilisant le fait que et ont des automorphismes supplémentaires en caractéristiques 2 et 3. (En gros, en caractéristique p, on peut ignorer les flèches de multiplicité p dans le diagramme de Dynkin lorsqu'on considère les automorphismes du diagramme). Le plus petit groupe de type est non simple, mais il possède un sous-groupe simple d'index 2, appelé le groupe de Tits (nommé en l'honneur du mathématicien belge Jacques Tits). Le plus petit groupe de type est non simple, mais il possède un sous-groupe normal d'index 3, isomorphe à . Dans la classification des groupes simples finis, les groupes de Ree

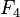
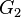
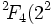
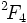
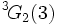
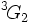
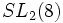
sont ceux dont la structure est la plus difficile à élucider explicitement. Ces groupes ont aussi joué un rôle dans la découverte du premier groupe sporadique moderne. Ils ont des centralisateurs d'involution de la forme Z/2Z × PSL₂(q) pour q = 3ⁿ, et en étudiant les groupes avec un centralisateur d'involution de forme similaire Z/2Z × PSL₂(5) Janko découvrit le groupe sporadique J₁.