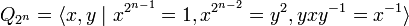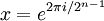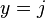Groupe des quaternions - Définition
La liste des auteurs de cet article est disponible ici.
Groupe de quaternions généralisé
Un groupe est appelé un groupe de quaternions généralisé s'il possède une présentation
pour un certain entier n ≥ 3. L'ordre de ce groupe est 2n. Le groupe de quaternions ordinaire correspond au cas n = 3. Le groupe de quaternions généralisé peut être réalisé comme le sous-groupe des quaternions unités engendré par
Un tel groupe peut être mis en relation avec un groupe diédral d'ordre 2n-1 par la suite exacte :
Les groupes de quaternions généralisés sont membres d'une famille encore plus large de groupes dicycliques (en). Les groupes de quaternions généralisés ont la propriété que chaque sous-groupe abélien est cyclique. On peut prouver qu'un p-groupe fini possédant cette propriété (chaque sous-groupe abélien est cyclique) est soit un groupe cyclique soit un groupe de quaternions généralisé comme défini ci-dessus.