Groupe cyclique - Définition

Introduction

En mathématiques et plus précisément en algèbre, un groupe cyclique, ou ce qui est équivalent, un groupe monogène, est un groupe dans lequel il existe un élément a tel que tout élément du groupe puisse (en notation additive) s'exprimer sous forme d'un multiple de a, cet élément a est appelé générateur du groupe. Il n'existe, à isomorphisme près, qu'un seul groupe cyclique infini : le groupe additif Z des entiers relatifs, et (pour tout entier naturel n>0) qu'un seul groupe cyclique d'ordre n : le quotient Z/nZ de Z par le sous-groupe des multiples de n. Les groupes cycliques sont importants en théorie des groupes et de manière générale en algèbre. On les retrouve, par exemple, en théorie des anneaux et dans la théorie de Galois.

Définitions

• Un groupe cyclique est un groupe monogène, i.e. engendré par un singleton. L'expression cycle pour désigner un groupe cyclique est aussi utilisée, mais comporte un risque de confusion avec la notion de permutation circulaire.
• Soit G un groupe et a un élément de G, alors le groupe engendré par a, noté <a>, est le plus petit sous-groupe de G contenant a.
• L'ordre d'un élément d'un groupe est l'ordre du sous-groupe engendré par cet élément. L'ordre de a est noté |a| ou o(a). Lorsqu'il est fini, on montre que c'est le plus petit entier n strictement positif tel que :
  • na = 0 (en notation additive),
  • a ⁿ = 1 (en notation multiplicative).

• Un élément primitif d'un groupe cyclique est un élément générateur.

Théorème fondamental

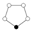
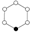
Les groupes cycliques possèdent une structure simple à comprendre. Ils forment une structure telle que les puissances d'un élément (en notation multiplicative), bien choisi, engendrent tout le groupe. Cette situation est illustrée dans la figure suivante, qui présentent les racines complexes de l'unité sur un cercle.

L'élément neutre est représenté par un point noir, un élément générateur peut être obtenu en prenant (par exemple) le premier élément en tournant vers la droite, le carré de cet élément générateur s'obtient en tournant toujours dans la même direction. Et ainsi de suite. L'élément n+1 est égal à l'élément 1, n+2 à l'élément 2, et ainsi de suite.

C_n désigne, suivant la convention habituelle, le groupe cyclique d'ordre n.

C1	C2	C3	C4	C5	C6	C7	C8

La traduction en termes mathématiques est alors la suivante :

• Soit G un groupe cyclique d'ordre n, alors G est isomorphe à Z/nZ.

Ce théorème est important, car il démontre la simplicité d'un groupe cyclique. À la fois, ce groupe est unique pour un ordre donné et, de plus, sa structure est limpide. De ce théorème découlent immédiatement quelques corollaires :

• Tout groupe cyclique est abélien.
• Soit G un groupe cyclique d'ordre p.q, où p et q sont deux entiers strictement positifs, alors il n'existe qu'un seul sous-groupe H d'ordre p et, si g est un élément primitif de G, alors g^q est un élément primitif de H.
• Le quotient d'un groupe cyclique par un sous-groupe quelconque est un groupe cyclique.
• Soit p un nombre premier : le groupe cyclique d'ordre p est le seul groupe d'ordre p, à un isomorphisme près.

• Soit G un groupe cyclique d'ordre n, alors G est isomorphe à Z/nZ>.

Si le groupe est cyclique, alors il contient au moins un élément primitif g. Considérons alors φ l'application de Z dans G qui à un entier p associe g ^p. Cette application est un morphisme de groupe, en effet:

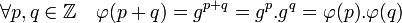
Par définition d'un groupe cyclique, le morphisme est surjectif. Donc la décomposition fondamentale des morphismes (cf morphisme de groupe) montre que G est isomorphe à au groupe quotient Z>/Ker φ. Le noyau de φ est non nul car sinon il existerait une bijection d'un ensemble de cardinal infini : Z avec un ensemble de cardinal fini G. Le noyau de φ est donc un sous-groupe non vide de Z>, il existe donc n un entier strictement positif tel que Ker φ = n.Z (cf paragraphe exemples de sous-groupes). La démonstration est donc achevée.

• Tout groupe cyclique est abélien.

La démonstration précédente montre l'existence d'un morphisme surjectif d'un groupe abélien : de Z vers le groupe cyclique. La propriété de commutativité du groupe de départ est donc transmise au groupe cyclique.

• Soit G un groupe cyclique d'ordre p.q, où p et q sont deux entiers strictement positifs, alors il n'existe qu'un seul sous-groupe H d'ordre p et, si g est un élément générateur de G, alors g^q est un élément générateur de H (qui est par conséquent cyclique).

Remarquons tout d'abord que tout élément g^r (comme g est générateur du groupe, pour tout élément du groupe, il existe un unique entier r compris entre 1 et p.q, tel qu'il est égal à g^r) d'un sous-groupe d'ordre p de G vérifie l'équation du théorème de Lagrange :

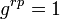
On en déduit que r.p est un multiple de p.q et, donc, r est un multiple de q. Il existe exactement p valeurs possibles de r, tel que r soit un multiple de q et soit compris entre 1 et p.q. Il n'existe donc que p candidats à être élément d'un sous-groupe d'ordre p. Il ne peut donc exister qu'un seul sous-groupe d'ordre p dans G.

Réciproquement, le sous-groupe engendré par g^q est un sous-groupe monogène à p éléments. Il existe donc bien un unique sous-groupe à p éléments, ce qui termine la démonstration.

• Le quotient d'un groupe cyclique par un sous-groupe quelconque est un groupe cyclique.

Les puissance d'un générateur du groupe parcourent l'intégralité du groupe, par passage au quotient, la classe du générateur engendre le groupe quotient.

• Pour p nombre premier, le seul groupe d'ordre p est le groupe cyclique d'ordre p à un isomorphisme près.

Soit g un élément du groupe d'ordre p. Il engendre un sous-groupe à au moins deux éléments 1 et g. Le théorème de Lagrange montre que le sous-groupe engendré par g a pour ordre un diviseur de p. Or, p n'a pas d'autre diviseur strictement supérieur à 1 que lui-même. Le sous-groupe engendré par g est donc le groupe entier. Il est donc monogène et d'ordre fini, c'est-à-dire cyclique.