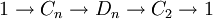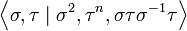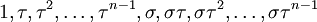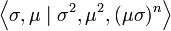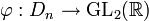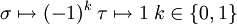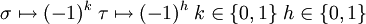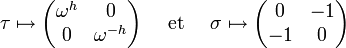Groupe diédral - Définition

Introduction

Symétrie bidimensionnelle D₄

En mathématiques, le groupe diédral noté D_n, pour , ou parfois D_2n, est un groupe d'ordre 2n qui s'interprète notamment comme le groupe des isométries du plan conservant un polygone régulier à n côtés. Le groupe est constitué de n éléments correspondant aux rotations et n autres correspondant aux réflexions. Le groupe D₁ est le groupe cyclique d'ordre 2, noté C₂ ; le groupe D₂ est le groupe de Klein à quatre éléments. Parmi les groupes diédraux D_n, ce sont les deux seuls à être abéliens.

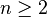
Présentation et définitions équivalentes

Le groupe D_n peut être défini par la suite exacte scindée suivante :

où C_n est un groupe cyclique d'ordre n, C₂ est cyclique d'ordre 2, la section étant donnée par l'action d'un relevé σ du générateur de C₂, sur un générateur τ du groupe cyclique d'ordre n :

στσ ^{− 1} = τ ^{− 1}

Ce groupe est donc produit semi-direct de C_n par C₂ suivant le morphisme ψ, où l'unité de C₂ agit sur C_n comme l'application identique et l'autre élément de C₂ agit sur C_n par inversion. Explicitement:

.

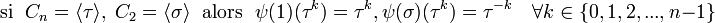
Une présentation est alors :

On peut ainsi dresser une liste complète des éléments du groupe :

Une présentation alternative, où μ = τσ dans le système de générateurs de la présentation précédente, est :

On voit ainsi que le groupe diédral admet un système de deux générateurs distincts tous deux d'ordre 2. Les groupes diédraux sont les seuls groupes finis possédant cette propriété.

Le groupe diédral d'ordre 2n peut aussi être vu comme le groupe d'automorphisme du graphe constitué seulement d'un cycle avec n sommets (si n ≥ 3).

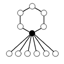
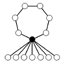
Graphe de cycle

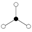
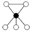
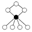
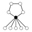
Les graphes de cycles de groupes diédraux sont constitués d'un cycle à n éléments et de cycles à 2 éléments. Le sommet sombre dans les graphes de cycle ci-dessous de divers groupes diédraux représente l'élément identité, et les autres sommets sont les autres éléments du groupe. Un cycle est constitué des puissances successives de l'un ou l'autre élément connecté à l'élément identité.

D2	D3	D4	D5	D6	D7

Interprétation géométrique

On peut définir de la façon suivante une représentation du groupe diédral D_n :

avec et . Cette représentation est en fait à valeurs dans le groupe .

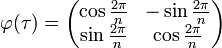
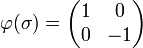
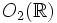
On reconnaît que la matrice φ(τ) est une matrice de rotation d'angle , et la matrice φ(σ) une matrice de réflexion. Ces transformations laissent effectivement invariant le polygone régulier centré en l'origine à n côtés.

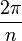
Représentations

Si n est impair, le groupe D_n admet 2 représentations irréductibles complexes de degré 1 :

En revanche, si n est pair, il existe 4 représentations irréductibles de degré 1 :

Les autres représentations irréductibles sont toutes de degré 2 ; elles sont en nombre si n est impair, respectivement si n est pair. On peut les définir comme suit :

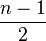
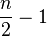
où ω désigne une racine primitive n^e de l'unité, et h parcourt les entiers compris entre 1 et n-1. On peut vérifier que deux telles représentations sont isomorphes seulement pour h₁ et h₂ vérifiant h₁+h₂=n. On obtient alors le nombre annoncé de représentations irréductibles de degré 2 non isomorphes, et donc toutes les représentations irréductible du groupe diédral, par la formule liant le nombre de représentations irréductibles à l'ordre du groupe.