Inégalité de réarrangement - Définition
La liste des auteurs de cet article est disponible ici.
Démonstration
La minoration est obtenue en appliquant la majoration à
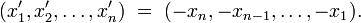
Il suffit donc de démontrer la majoration. Comme
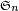
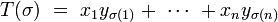
soit maximal. Si il existe plusieurs permutations maximales, notons σ une des permutations maximales, choisie parmi les permutations maximales qui possèdent le plus grand nombre de points fixes (s'il y en a plusieurs).
On va démontrer par l'absurde que σ est nécessairement l'élément identité de
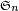
![\scriptstyle\ [\![1,n]\!]\](https://static.techno-science.net/illustration/Definitions/autres/2/2f13ba6ef79e2c256c822e67f6e5a85f_eaf079bf872d4a443f973513a8981f8a.png)
![\scriptstyle\ [\![1,j-1]\!]\](https://static.techno-science.net/illustration/Definitions/autres/e/e5d8a15f37e3d54f7e84d5556f7a6cc4_8d5983694c287c155ffa9a1eca9b5d0e.png)
![\scriptstyle\ [\![1,n]\!]\](https://static.techno-science.net/illustration/Definitions/autres/2/2f13ba6ef79e2c256c822e67f6e5a85f_eaf079bf872d4a443f973513a8981f8a.png)
![\scriptstyle\ [\![1,j-1]\!]\](https://static.techno-science.net/illustration/Definitions/autres/e/e5d8a15f37e3d54f7e84d5556f7a6cc4_8d5983694c287c155ffa9a1eca9b5d0e.png)
![\scriptstyle\ k\in[\![j+1,n]\!]\](https://static.techno-science.net/illustration/Definitions/autres/8/8d9e597989ca690ace99ce346615643e_31e5a6015372eb1297916d4d357fc389.png)
![\scriptstyle\ [\![1,j-1]\!]\](https://static.techno-science.net/illustration/Definitions/autres/e/e5d8a15f37e3d54f7e84d5556f7a6cc4_8d5983694c287c155ffa9a1eca9b5d0e.png)
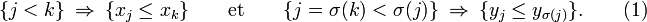
Par conséquent,
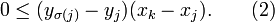
En développant et en réordonnant, on obtient :
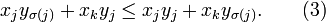
On remarque que la permutation τ définie par
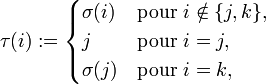
obtenue à partir de σ en échangeant les valeurs de σ(j) et σ(k), possède au moins un point fixe de plus que σ, à savoir j, et aucun point fixe de moins puisque le seul autre élément dont l'image change, l'élément k, n'était pas un point fixe. De plus, les deux sommes,
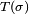
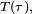
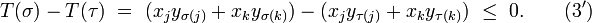
Finalement, (3') est en contradiction avec le choix de σ.
Si
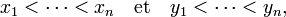
alors les inégalités (1), (2), et (3) sont strictes, donc le maximum ne peut être atteint qu'en l'identité, tout autre permutation τ étant strictement suboptimale.

















































