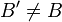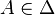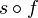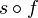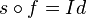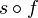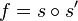Isométrie affine - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Classification des isométries planes ayant un point fixe
- Une isométrie du plan ayant trois points fixes non alignés est l'identité.
- Une isométrie du plan autre que l'identité ayant au moins deux points fixes A et B est la réflexion par rapport à la droite (AB).
- Une isométrie du plan ayant un unique point fixe A est une rotation de centre A.
- Soit f une isométrie plane autre que l'identité. Soit M un point du plan et M' = f(M) tel que
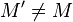
- Soit f une isométrie plane autre que l'identité ayant au moins deux points fixes A et B et s la réflexion par rapport à la droite (AB). Soit C un point n'appartenant pas à (AB). Alors son image C' par f vérifie CA = C'A et CB = C'B donc C' appartient à l'intersection de deux cercles de centres respectifs A et B. Cette intersection a au plus deux points et C' est différent de C (sinon f aurait trois points fixes non alignés et serait l'identité, ce qui est exclu par hypothèse) donc C et C' sont les deux points d'intersection respectifs de ces cercles (rappelons que deux cercles de centres distincts ont au plus deux points en commun). Comme CA = C'A et CB = C'B, A et B sont sur la médiatrice de [CC']; par définition, on a donc s(C') = C. Comme s(A) = A et s(B) = B,
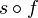
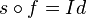
- Si f possède un unique point fixe A: soit B un point distinct de A et B' = f(B). On a alors