Point fixe - Définition

En mathématiques, pour une application f d’un ensemble E dans lui-même, un élément x de E est un point fixe de f si f(x) = x.

Exemples :

• dans le plan, la symétrie par rapport à un point A admet un unique point fixe : A
• l’application inverse (définie sur l’ensemble des réels non nuls) admet deux points fixes : -1 et 1

Graphiquement, les points fixes d’une fonction f (où la variable est réelle) s’obtient en traçant la droite d’équation y = x : tous les points d’intersection de la courbe représentative de f avec cette droite sont alors les points fixes de f.

Toutes les fonctions n’ont pas nécessairement de point fixe; par exemple, la fonction n’en possède pas, car il n’existe aucun nombre réel x égal à x+1.

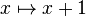
Point fixe et suites récurrentes

On considère la fonction continue et (u_n) la suite récurrente définie par sa valeur initiale u₀ et par la relation de récurrence u_n+1=f(u_n). Dans ce cas, si (u_n) converge, elle le fait nécessairement vers un point fixe de f.

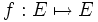
Il faut noter qu’une telle suite ne converge pas forcément, même si f possède un point fixe.

Point fixe attractif

Un point fixe attractif d’une application f est un point fixe x₀ de f tel qu’il existe un voisinage de x₀ sur lequel la suite de nombre réels

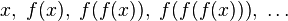
converge vers x₀.

Par exemple, la fonction cosinus admet un unique point fixe, qui est attractif.

Cependant, tous les points fixes d’une fonction ne sont pas nécessairement attractifs. Ainsi, la fonction réelle possède un unique point fixe en 0, qui n’est pas attractif.

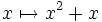
Les points fixes attractifs sont un cas particulier du concept mathématique d’attracteur.

Théorèmes du point fixe

Il existe plusieurs théorèmes permettant de déterminer qu’une application satisfaisant à certains critères possède un point fixe. Le plus connu est le suivant :

Soit E un espace métrique complet muni d’une distance d et une application contractante (c’est-à-dire qu’il existe tel que pour tous , ). Alors f possède un unique point fixe l.

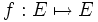
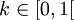
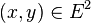
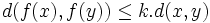
Ce résultat permet de dire que toute suite de la forme u_{n + 1} = f(u_n) converge vers l et que , ce qui permet d’avoir une estimation de la vitesse de convergence de la suite.

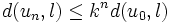
Utilisation en automatique

L’automatique consiste à fabriquer des systèmes qui convergent vers un point fixe (mais réglé arbitrairement par l’opérateur) et qui se nomme le point de consigne.