Isométrie affine - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Isométries planes remarquables - En dimension quelconque - Classification des isométries planes ayant un point fixe

Introduction

Une isométrie affine est une transformation bijective d'un espace affine euclidien dans un autre qui est à la fois une application affine et une isométrie (c'est-à-dire une bijection conservant les distances).

Si cette isométrie conserve aussi les angles orientés, alors il s'agit d'un déplacement. Si elle inverse les angles orientés, il s'agit d'un antidéplacement.

Isométries planes remarquables

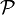
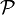
On désigne par $\mathcal{P}$ le plan (i.e., plus précisément, un plan affine réel euclidien orienté). Les applications suivantes sont des isométries de $\mathcal{P}$ :

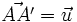
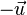
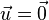
Étant donné un vecteur $\vec{u}$ l'application qui, à tout point $A$ , associe le point $A'$ tel que $\vec{AA'}=\vec{u}$ : c'est la translation de vecteur $\vec{u}$ . Sa réciproque est la translation de vecteur $-\vec{u}$ . Elle n'a aucun point fixe, sauf si $\vec{u}=\vec{0}$ , auquel cas c'est l'identité. Les translations sont des déplacements.
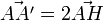
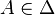
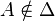
Étant donnée une droite $Δ$ l'application qui, à tout point $A$ , associe le point $A'$ tel que $\vec{AA'}=2\vec{AH}$ , où $H$ est le projeté orthogonal de $A$ sur $Δ$ : c'est la réflexion d'axe $Δ$ . On peut la définir autrement : si $A \in \Delta$ alors $A' = A$ et si $A \notin \Delta$ alors $A'$ est tel que $Δ$ est la médiatrice de $[A A']$ . Les réflexions sont involutives et sont des antidéplacements.
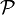
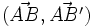
Étant donné un point $A$ de $\mathcal{P}$ et un réel $θ$ l'application qui fixe $A$ et, à un point $B$ distinct de $A$ , associe l'unique point $B'$ tel que $A B = A B'$ et une mesure de l'angle orienté $(\vec{AB}, \vec{AB'})$ est $θ$ : c'est la rotation de centre $A$ et d'angle $θ$ . La réciproque de la rotation de centre $A$ et d'angle $θ$ est la rotation de centre $A$ et d'angle $- θ$ . Enfin, les rotations sont des déplacements.

En dimension quelconque

Une application d'un espace euclidien dans lui-même qui conserve les distances conserve nécessairement l'alignement. D'après le théorème fondamental de la géométrie affine, c'est par conséquent une application affine, et son application linéaire associée conserve la norme donc est un automorphisme orthogonal. Réciproquement, toute application affine dont l'application linéaire associée est un automorphisme orthogonal est une isométrie affine.

Les automorphismes orthogonaux sont caractérisés par le fait que leur matrice dans une base orthonormée est une matrice orthogonale.

Parmi les isométries affines on distingue, de même que parmi les automorphismes orthogonaux, les déplacements (isométries affines directes), qui conservent l'orientation, et les antidéplacements (isométries affines indirectes), qui la renversent. Le déterminant de la matrice précitée vaut respectivement +1 ou -1. Les antidéplacements sont aussi appelés antirotations ou roto-inversions.^{[réf. souhaitée]}

Exemples. Les translations sont des déplacements sans point fixe. En dimension 2 ou 3, une rotation affine est un déplacement ayant au moins un point fixe. Dans le plan, les antidéplacements sont les réflexions et les réflexions glissées.

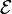
Pour étudier les isométries affines en dimension quelconque, on s'intéresse à l'automorphisme orthogonal $φ$ associé défini de la sorte : si $f : \begin{array}[t]{lcl}\mathcal{E} &\rightarrow & \mathcal{E} \\ M & \mapsto & f(M) \end{array}$ est une isométrie affine de $\mathcal{E}$ , alors son automorphisme orthogonal associé est $\phi : \begin{array}[t]{lcl}E &\rightarrow & E \\ \overrightarrow{MN} & \mapsto & \overrightarrow{f(M)f(N)} \end{array}$ Dès lors l'étude des points fixes de $f$ et de $φ$ permet de conclure sur la nature de $f$ .