Médiatrice - Définition

Introduction

En géométrie plane, la médiatrice d'un segment est l'ensemble des points équidistants des extrémités du segment. Cet ensemble est la droite passant par le milieu du segment et qui est perpendiculaire au segment. La médiatrice d'un segment [AB] divise donc le plan en deux demi-plans. Les points plus proches de A que de B sont dans un des demi-plans et les points plus proches de B que de A sont dans l'autre. Ainsi les frontières du diagramme de Voronoï sont des segments de médiatrices.

Propriétés

Dans un triangle, les médiatrices des trois côtés sont concourantes en un point qui est le centre du cercle circonscrit de ce triangle.

La médiatrice d'un segment est un axe de symétrie de ce segment. Dans un rectangle, les médiatrices des côtés sont également des axes de symétries du rectangle.

Construction au compas et à la règle

Cette construction est attribuée à Œnopide de Chios. Elle permet de construire la médiatrice d'un segment à l'aide d'une règle et d'un compas. On n'utilise donc pas d'équerre ou de règle graduée.

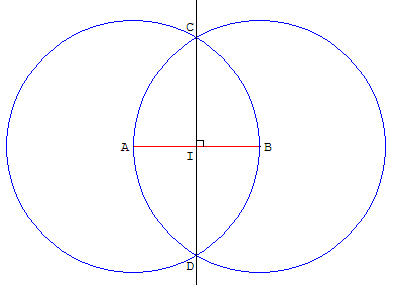
Soit le segment [AB]. On règle d'abord le compas à un rayon quelconque, supérieur à la moitié de la longueur AB. Avec cet écartement de compas, on trace un cercle centré sur A, puis un cercle de même rayon centré sur B. Ces deux cercles se coupent en deux points C et D. On trace enfin la droite (CD) qui est la médiatrice de [AB].

Construction d'une médiatrice au compas et à la règle non graduée

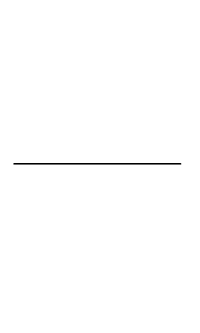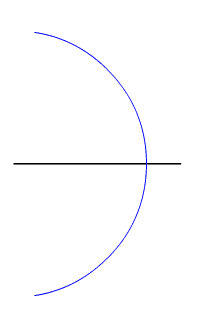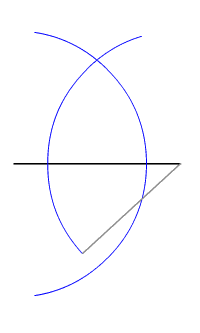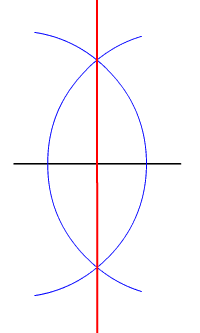
En effet, comme rayons des cercles CA = CB et DA = DB. Les points C et D sont donc deux points distincts de la médiatrice. La droite passant par C et D est nécessairement la médiatrice de [AB].

Intérêt de cette construction

Construction d'une perpendiculaire à une droite passant par un point donné.

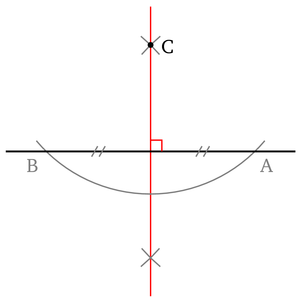
Cette construction est habituellement privilégiée pour sa meilleure précision en comparaison à l'utilisation de la règle et de l'équerre puisqu'il n'est pas nécessaire de mesurer le segment pour en trouver le milieu.

Cette construction permet de tracer la perpendiculaire à une droite donnée passant par un point donné. Ainsi toute construction à l'équerre est réputée réalisable à la règle et au compas seulement.

Considérons une droite (D) et un point C extérieur à cette droite. On commence par tracer un cercle de centre C qui va couper la droite (D) en deux points A et B. Grâce à la construction précédente, on construit la médiatrice de [AB]. Comme C est à égale distance de A et B, C est sur cette médiatrice. Ainsi la médiatrice de [AB] est la droite perpendiculaire à (D) et passant par C.