Lemme de l'étoile - Définition

Preuve du lemme de l'étoile

Rappel : si L est un langage rationnel, alors il existe un automate fini reconnaissant le langage L.

On considère un langage rationnel L.

Premier cas : si L est fini, alors on choisit . Alors il n'existe pas de mot w appartenant à L tel que , donc l'assertion à vérifier est triviale.

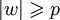
Deuxième cas : si L est infini.
Il existe un automate fini A qui reconnaît L. Le nombre d'états de A étant fini, on note p ce nombre augmenté de 1.
Soit maintenant w un mot de L tel que . w est reconnu par A, donc il existe un chemin réussi dans A, étiqueté par w. Autrement dit, q₀ est un état initial de A, et en partant de cet état on peut lire l'une après l'autre toutes les lettres de w en terminant la lecture par un état q_n acceptant de A. Ceci impose , ce qui assure par la définition de p qu'un certain état intervient au moins deux fois dans le chemin parcouru pour lire w.
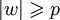
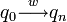
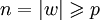
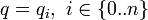
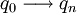
On peut choisir i minimal. q est ainsi décrit comme la première occurrence du premier état q répété au cours du chemin . On note alors y le mot qui est lu entre q_i et q_j, la deuxième occurrence de q dans le chemin en question (avec donc ). On note x le mot lu entre q₀ et q_i, et z le mot lu entre q_j et q_n. Ainsi, w = xyz.
On remarque que x et z peuvent être vides, mais y ne l'est pas. Vu la définition de y, la propriété (4) du lemme est vérifiée. Quant à la propriété (2), elle résulte des choix de i et j.