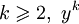Lemme de l'étoile - Définition

Introduction

En théorie des langages, le lemme de l'étoile (ou encore lemme d'itération, lemme de pompage, pumping lemma en anglais) décrit une propriété essentielle de tout langage rationnel. Informellement, il établit que tout mot suffisamment long d'un langage rationnel peut être pompé, c'est-à-dire qu'une partie centrale du mot peut être répétée un nombre arbitraire de fois pour produire un nouveau mot qui se trouve encore dans le langage initial.

Le lemme de l'étoile a été imaginé pour la première fois par Y. Bar-Hillel, Micha A. Perles, Eli Shamir en 1961. Il est très pratique pour montrer qu'un langage donné n'est pas rationnel (en raisonnant par l'absurde).

Énoncé formel

Soit L un langage rationnel sur l'alphabet X.

Alors il existe un entier p tel que :

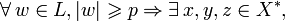
1. w = xyz,
2. 
3. 
4. 

désigne la longueur du mot w. L'entier p ne dépend que de L et est parfois appelé "longueur de pompage". (1) signifie que w est divisé en trois facteurs ; (2) signifie que y doit être de longueur au moins 1 ; (3) signifie que la "pompe" y doit se trouver dans les p premières lettres de w. Il n'y a pas de restrictions sur x et z.

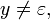
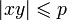
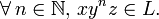
Considérations intuitives

Voici un automate fini reconnaissant le langage décrit par l'expression rationnelle a(bc)*d.

L'automate fini reconnaît le mot abcbcd. Comme il contient plus de lettres que le nombre d'états de l'automate, tout chemin étiqueté par abcbcd dans l'automate comportera au moins un état répété. Ici, l'état q₁ est répété. On comprend ainsi que ad appartient au langage reconnu par l'automate, en empruntant le chemin . De même, en répétant la boucle bc, tout mot de la forme a(bc)ⁿd avec sera reconnu par l'automate.

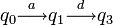
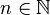
On pressent donc que la démonstration reposera sur le nombre d'état d'un automate reconnaissant le langage rationnel en question, et sur la répétition d'états lors de la lecture d'un mot.

Une application du lemme de l'étoile

Le lemme de l'étoile est souvent utilisé pour démontrer qu'un langage donné n'est pas rationnel. La preuve se fait en général par l'absurde, en supposant que le langage est rationnel et en exhibant un mot du langage de longueur suffisante tel que la propriété (4) du lemme n'est pas vérifiée.

Prenons par exemple le langage sur l'alphabet Σ = {a,b}. Supposons par l'absurde que L est rationnel. On fixe l'entier p apparaissant dans l'énoncé du lemme. On choisit le mot w = a^pb^p. Il existe donc une décomposition(d´apres la condition (1) du lemme) w = xyz vérifiant les conditions (2), (3), (4)du lemme de l'étoile. | xy | < p donc il existe deux entiers i et j tels que i + j < p et x = aⁱ,y = a^j. De plus j > 0 car y n'est pas le mot vide. Il en résulte que z = a^{p − i − j}b^p. On devrait ainsi avoir , ce qui est absurde car p − j < p. Donc L n'est pas rationnel.

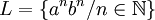
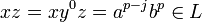
On montre de même que

• le langage des palindromes sur Σ = {a,b} n'est pas rationnel,
• le langage sur Σ = {a,b} n'est pas rationnel (où | w | _a désigne le nombre d'occurrences de la lettre a dans le mot w).

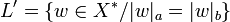
Une condition nécessaire mais non suffisante

Il faut bien saisir que le lemme ne donne qu'une condition nécessaire. La contraposée de ce lemme nous dit donc qu'un langage ne vérifiant pas les propriétés énoncées n'est pas rationnel, mais en aucun cas on ne peut affirmer qu'un langage non rationnel ne vérifiera pas ces propriétés. Il s'agit d'un problème d'implication logique, entre autres :

• Si le lemme est faux pour un langage donné, alors ce langage n'est pas rationnel
• Si le lemme est vrai pour un langage donné, alors ce langage peut ne pas être rationnel

Par exemple, notons u^R l'image miroir d'un mot quelconque u. u^R est donc tel que uu^R est un palindrome. Le langage n'est pas rationnel et vérifie le lemme. Plus explicitement, L est le langage des mots constitués d'un palindrome non vide suivi d'un mot non vide sur l'alphabet {a,b}.
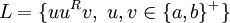
Prenons p = 4, et w = uu^Rv de longueur au moins 4. Si u est de longueur 1, alors v est de longueur au moins 2, et on choisit pour y la première lettre de v par exemple. Sinon, u est de longueur au moins 2 et on prend pour y la première lettre de u, z les lettres restantes et x le mot vide : on remarque que pour commence par le palindrome non vide yy.