Localisation (mathématiques) - Définition

Localisation de modules

Soient A et S comme avant. Soit M un A-module. Alors la localisation S ^{− 1}M est un S ^{− 1}A-module muni d'un homomorphisme A-linéaire tel que tout homorphisme A-linéaire dans un S ^{− 1}A-module N se factorise de façon unique en composé de f avec un homomorphisme S ^{− 1}A-linéaire . Concrètement, S ^{− 1}M est l'ensemble modulo la relation d'équivalence: si set seulement s'il existe t dans S tel que t(s'x − sx') = 0. L'application canonique consiste à envoyer x sur la classe de (x,1). Son noyau est le sous-module des x annulé par un élément de S.

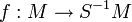
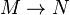
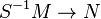
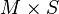
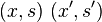
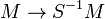
On peut montrer que S ^{− 1}M est isomorphe au produit tensoriel de M et S ^{− 1}A sur A.

Spectre d'une localisation

Soit S une partie multiplicative de A. Alors l'ensemble des idéaux premiers de S ^{− 1}A peut s'identifier à la partie des idéaux premiers de A disjoints de S. Plus précisément, soit le morphisme canonique. Pour tout idéal premier Q de S ^{− 1}A, est un idéal premier de A qui est disjoint de S, et cette correspondance est biunivoque, la correspondance réciproque associant un idéal premier P de A l'idéal I(P)S ^{− 1}A de S ^{− 1}A. De plus, le morphisme canonique entre les anneaux intègres induit un isomorphisme entre leurs corps des fractions.

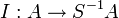
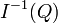
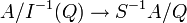
Noter qu'en général, cette correspondance n'existe pas pour les idéaux maximaux (considérer l'exemple avec A égal à l'anneau des entiers et S ^{− 1}A son corps des fractions).