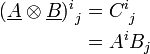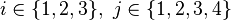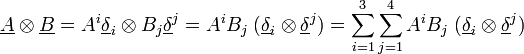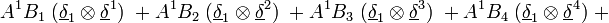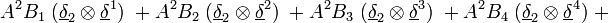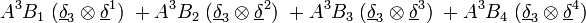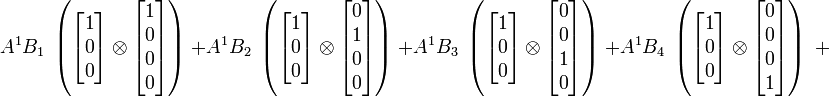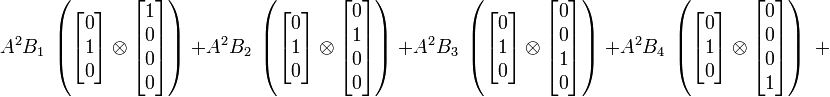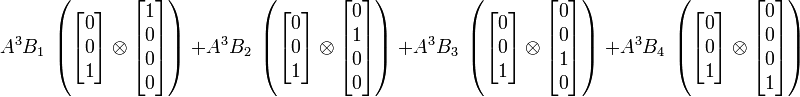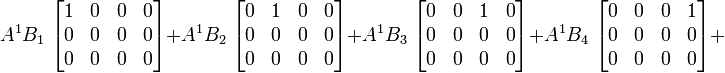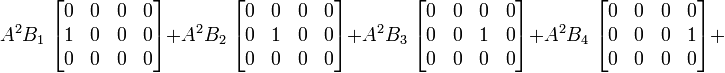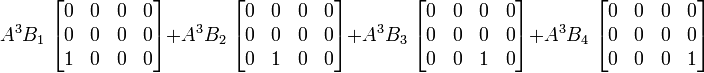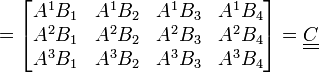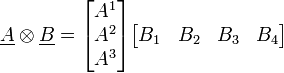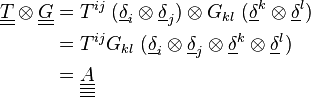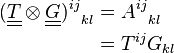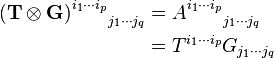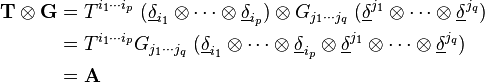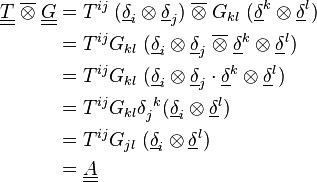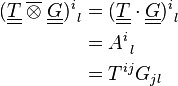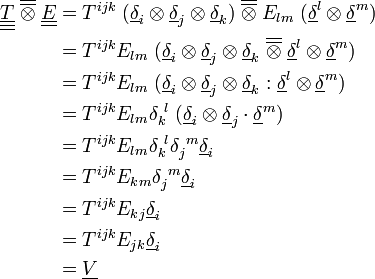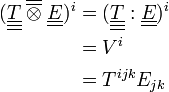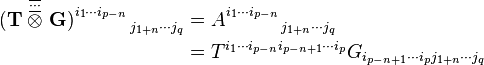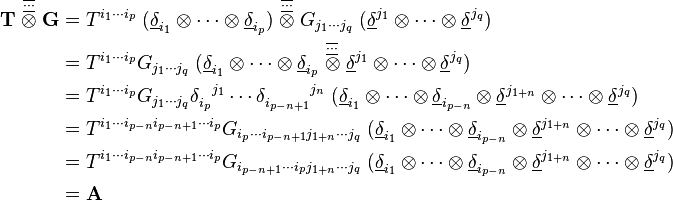Samedi 14 Décembre 2024
Rechercher 🔍

Produit tensoriel - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Produit tensoriel - Produit tensoriel contracté

Introduction

Articles scientifiques
sur les tenseurs
Généralités

Tenseur

Mathématiques

Tenseur (mathématiques)
Produit tensoriel
... de deux modules
... de deux applications linéaires
Algèbre tensorielle
Champ tensoriel
Espace tensoriel

Convention d'Einstein
Tenseur métrique
Tenseur énergie-impulsion
Tenseur de Riemann
... de Ricci
... d'Einstein
... de Weyl
... de Levi-Civita
... de Killing
... de Killing-Yano
... de Bel-Robinson
... de Cotton-York
Tenseur électromagnétique
Tenseur des contraintes
Tenseur des déformations

Articles connexes

Modules
Algèbre extérieure

Portail des Mathématiques
Portail de la Physique

On appelle produit tensoriel, ou produit de Kronecker, le produit de chaque composante d'un tenseur par chaque composante d'un autre tenseur. Le produit d'un tenseur d'ordre p avec un tenseur d'ordre q est un tenseur d'ordre p + q (si le produit n'est pas contracté).

Le produit tensoriel n'est pas commutatif mais pseudo-commutatif.

Produit tensoriel

Les exemples ci-dessous emploient la convention de sommation d'Einstein.

Avec cette convention, on n'écrit pas les sommations qui deviennent très vite lourdes à traîner. On somme les indices répétés deux fois de la quantité appropriée.

Attention, les formules des produits tensoriels en termes de composantes ne sont valables que si les tenseurs sont exprimés par rapport à une base orthonormée.

Les formules des produits tensoriels en termes de composantes fonctionnent toujours sur des tenseurs d'ordre 1 formant une base car une base quelconque est toujours exprimée en fonction d'une base orthonormée.

Produit tensoriel de deux tenseurs d'ordre 1 (vecteurs)

En termes de composantes :

\begin{align} (\underline A \otimes \underline B)^i_{\ j} &= C^i_{\ j} \\ &= A^iB_j \end{align}

En termes tensoriel :

i \in \{1,2,3\},~j \in \{1,2,3,4\}
\underline A \otimes \underline B = A^i \underline\delta_i \otimes B_j \underline\delta^j = A^i B_j \; (\underline\delta_i \otimes \underline\delta^j) = \sum_{i=1}^3 \sum_{j=1}^4 A^i B_j \; (\underline\delta_i \otimes \underline\delta^j)
=~
A^1 B_1 \; (\underline\delta_1 \otimes \underline\delta^1) \; + A^1 B_2 \; (\underline\delta_1 \otimes \underline\delta^2) \; + A^1 B_3 \; (\underline\delta_1 \otimes \underline\delta^3) \; + A^1 B_4 \; (\underline\delta_1 \otimes \underline\delta^4) \; +
A^2 B_1 \; (\underline\delta_2 \otimes \underline\delta^1) \; + A^2 B_2 \; (\underline\delta_2 \otimes \underline\delta^2) \; + A^2 B_3 \; (\underline\delta_2 \otimes \underline\delta^3) \; + A^2 B_4 \; (\underline\delta_2 \otimes \underline\delta^4) \; +
A^3 B_1 \; (\underline\delta_3 \otimes \underline\delta^1) \; + A^3 B_2 \; (\underline\delta_3 \otimes \underline\delta^2) \; + A^3 B_3 \; (\underline\delta_3 \otimes \underline\delta^3) \; + A^3 B_4 \; (\underline\delta_3 \otimes \underline\delta^4) \;
=~
A^1 B_1 \; \left ( \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} \otimes \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} \right ) \; + A^1 B_2 \; \left ( \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} \otimes \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix} \right ) \; + A^1 B_3 \; \left ( \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} \otimes \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \end{bmatrix} \right ) \; + A^1 B_4 \; \left ( \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} \otimes \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix} \right ) \; +
A^2 B_1 \; \left ( \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} \otimes \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} \right ) \; + A^2 B_2 \; \left ( \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} \otimes \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix} \right ) \; + A^2 B_3 \; \left ( \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} \otimes \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \end{bmatrix} \right ) \; + A^2 B_4 \; \left ( \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} \otimes \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix} \right ) \; +
A^3 B_1 \; \left ( \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \otimes \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix} \right ) \; + A^3 B_2 \; \left ( \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \otimes \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix} \right ) \; + A^3 B_3 \; \left ( \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \otimes \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \end{bmatrix} \right ) \; + A^3 B_4 \; \left ( \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix} \otimes \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix} \right ) \;
=~
A^1 B_1 \; \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} + A^1 B_2 \; \begin{bmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} + A^1 B_3 \; \begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} + A^1 B_4 \; \begin{bmatrix} 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} +
A^2 B_1 \; \begin{bmatrix} 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} + A^2 B_2 \; \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} + A^2 B_3 \; \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} + A^2 B_4 \; \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \end{bmatrix} +
A^3 B_1 \; \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{bmatrix} + A^3 B_2 \; \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{bmatrix} + A^3 B_3 \; \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix} + A^3 B_4 \; \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}
= \begin{bmatrix}A^1B_1 & A^1B_2 & A^1B_3 & A^1B_4 \\ A^2B_1 & A^2B_2 & A^2B_3 & A^2B_4 \\ A^3B_1 & A^3B_2 & A^3B_3 & A^3B_4\end{bmatrix} = \underline{\underline C}

On remarque que l'on peut exprimer ce produit tensoriel par un produit matriciel :

\underline A \otimes \underline B = \begin{bmatrix} A^1 \\ A^2 \\ A^3 \end{bmatrix} \begin{bmatrix} B_1 & B_2 & B_3 & B_4 \end{bmatrix}

Produit tensoriel de deux tenseurs d'ordre 2 (matrices)

En termes tensoriel :

\begin{align} \underline{\underline T} \otimes \underline{\underline G} &= T^{ij} \; (\underline \delta_i \otimes \underline \delta_j) \otimes G_{kl} \; (\underline \delta^k \otimes \underline \delta^l) \\ &= T^{ij} G_{kl} \; (\underline \delta_i \otimes \underline \delta_j \otimes \underline \delta^k \otimes \underline \delta^l) \\ &= \underline{\underline{\underline{\underline A}}} \end{align}

En termes de composantes :

\begin{align} (\underline{\underline T} \otimes \underline{\underline G})^{ij}_{\ \ kl} &= A^{ij}_{\ \ kl} \\ &= T^{ij}G_{kl} \end{align}

Produit tensoriel d'un tenseur d'ordre p et d'un tenseur d'ordre q

En termes de composantes :

\begin{align}(\mathbf{T} \otimes \mathbf{G})^{i_1 \cdots i_p}_{\ \ \ \ \ \; j_1 \cdots j_q} &= A^{i_1 \cdots i_p}_{\ \ \ \ \ \; j_1 \cdots j_q} \\ &= T^{i_1 \cdots i_p} G_{j_1 \cdots j_q} \end{align}

En termes tensoriel :

\begin{align}\mathbf{T} \otimes \mathbf{G} &= T^{i_1 \cdots i_p} \; (\underline\delta_{i_1} \otimes \cdots \otimes \underline\delta_{i_p}) \otimes G_{j_1 \cdots j_q} \; (\underline\delta^{j_1} \otimes \cdots \otimes \underline\delta^{j_q}) \\ &= T^{i_1 \cdots i_p} G_{j_1 \cdots j_q} \; (\underline\delta_{i_1} \otimes \cdots \otimes \underline\delta_{i_p} \otimes \underline\delta^{j_1} \otimes \cdots \otimes \underline\delta^{j_q}) \\ &= \mathbf{A} \end{align}

Produit tensoriel contracté

Produit tensoriel contracté une fois

On définit aussi le produit tensoriel contracté une fois comme ceci.

\begin{align} \underline{\underline T} \; \overline \otimes \; \underline{\underline G} &= T^{i j} \; (\underline \delta_i \otimes \underline \delta_j) \; \overline \otimes \; G_{k l} \; (\underline \delta^k \otimes \underline \delta^l) \\ &= T^{i j} G_{k l} \; (\underline \delta_i \otimes \underline \delta_j \; \overline \otimes \; \underline \delta^k \otimes \underline \delta^l) \\ &= T^{i j} G_{k l} \; (\underline \delta_i \otimes \underline \delta_j \cdot \underline \delta^k \otimes \underline \delta^l) \\ &= T^{i j} G_{k l} \delta_j^{\ k} (\underline\delta_i \otimes \underline\delta^l) \\ &=T^{i j} G_{j l} \; (\underline\delta_i \otimes \underline\delta^l) \\ &= \underline{\underline A} \end{align}

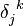
Le symbole \delta_j^{\ k} est appelé le delta de Kronecker

En termes de composantes :

\begin{align} ( \underline{\underline T} \; \overline\otimes \; \underline{\underline G} )^i_{\ l} &= (\underline{\underline T} \cdot \underline{\underline G} )^i_{\ l} \\ &= A^i_{\ l} \\ &= T^{i j} G_{j l} \end{align}

On procède de la même manière pour des tenseurs d'ordre différent.

Produit tensoriel contracté deux fois

On peut aussi effectuer un produit tensoriel contracté 2, 3, 4..., n fois. Ici, un exemple pour un produit contracté 2 fois entre un tenseur d'ordre 3 et un d'ordre 2.

\begin{align}\underline{\underline{\underline T}} \; \overline{\overline\otimes} \; \underline{\underline E} &= T^{i j k} \; (\underline\delta_i \otimes \underline\delta_j \otimes \underline\delta_k) \; \overline{\overline\otimes} \; E_{l m} \; (\underline\delta^l \otimes \underline\delta^m) \\ &= T^{i j k} E_{l m} \; (\underline\delta_i \otimes \underline\delta_j \otimes \underline\delta_k \; \overline{\overline\otimes} \; \underline\delta^l \otimes \underline\delta^m) \\ &= T^{i j k} E_{l m} \; (\underline\delta_i \otimes \underline\delta_j \otimes \underline\delta_k : \underline\delta^l \otimes \underline\delta^m) \\ &= T^{i j k} E_{l m} \delta_k^{\ l} \; (\underline\delta_i \otimes \underline\delta_j \cdot \underline\delta^m) \\ &= T^{i j k} E_{l m} \delta_k^{\ l} \delta_j^{\ m} \underline\delta_i \\ &= T^{i j k} E_{k m} \delta_j^{\ m} \underline\delta_i \\ &= T^{i j k} E_{k j} \underline\delta_i \\ &= T^{i j k} E_{j k} \underline\delta_i \\ &=\underline V \end{align}

Attention, Ejk n'est pas forcément égal à Ekj mais ici il y a sommation sur les indices j et k, l'ordre des indices n'importe donc pas.

En termes de composantes :

\begin{align} ( \underline{\underline{\underline T}} \; \overline{\overline\otimes} \; \underline{\underline E} )^i &= (\underline{\underline{\underline T}} : \underline{\underline E})^i \\ &= V^i \\ &= T^{i j k} E_{j k} \end{align}


Ici le résultat est un tenseur d'ordre 1 c'est-à-dire un vecteur. L'ordre du tenseur se calcule comme suit : O = P + Q − 2(n) Où O est l'ordre du nouveau tenseur, P et Q ceux du premier et deuxième tenseur alors que (n) est le nombre de fois que le produit est contracté.


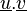
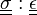
On utilise aussi pour le produit contracté la notation suivante : un point entre les tenseurs, comme pour le produit scalaire classique \underline{u} . \underline{v} Pour les produits contractés multiples, on note l'opération avec des points superposés (autant de point que de contraction dans le produit). Ainsi, le double-produit contracté se note \underline{\underline{\sigma}}:\underline{\underline{\epsilon}} .

Produit tensoriel contracté n fois d'un tenseur d'ordre p et d'un tenseur d'ordre q

En termes de composantes :

\begin{align}(\mathbf{T} \; \overset{\overline{\underline\cdots}}{\otimes} \; \mathbf{G})^{i_1 \cdots i_{p-n}}_{\ \ \ \ \ \ \ \ \; j_{1+n} \cdots j_q} &= A^{i_1 \cdots i_{p-n}}_{\ \ \ \ \ \ \ \ \; j_{1+n} \cdots j_q} \\ &= T^{i_1 \cdots i_{p-n} i_{p-n+1} \cdots i_p} G_{i_{p-n+1} \cdots i_p j_{1+n} \cdots j_q} \end{align}

En termes tensoriel :

\begin{align}\mathbf{T} \; \overset{\overline{\underline\cdots}}{\otimes} \; \mathbf{G} &= T^{i_1 \cdots i_p} \; (\underline\delta_{i_1} \otimes \cdots \otimes \underline\delta_{i_p}) \; \overset{\overline{\underline\cdots}}{\otimes} \; G_{j_1 \cdots j_q} \; (\underline\delta^{j_1} \otimes \cdots \otimes \underline\delta^{j_q}) \\ &= T^{i_1 \cdots i_p} G_{j_1 \cdots j_q} \; (\underline\delta_{i_1} \otimes \cdots \otimes \underline\delta_{i_p} \; \overset{\overline{\underline\cdots}}{\otimes} \; \underline\delta^{j_1} \otimes \cdots \otimes \underline\delta^{j_q}) \\ &= T^{i_1 \cdots i_p} G_{j_1 \cdots j_q} \delta_{i_p}^{\ \ j_1} \cdots \delta_{i_{p-n+1}}^{\ \ \ \ \ \ \ j_n} \; (\underline\delta_{i_1} \otimes \cdots \otimes \underline\delta_{i_{p-n}} \otimes \underline\delta^{j_{1+n}} \otimes \cdots \otimes \underline\delta^{j_q}) \\ &= T^{i_1 \cdots i_{p-n} i_{p-n+1} \cdots i_p} G_{i_p \cdots i_{p-n+1} j_{1+n} \cdots j_q} \; (\underline\delta_{i_1} \otimes \cdots \otimes \underline\delta_{i_{p-n}} \otimes \underline\delta^{j_{1+n}} \otimes \cdots \otimes \underline\delta^{j_q}) \\ &= T^{i_1 \cdots i_{p-n} i_{p-n+1} \cdots i_p} G_{i_{p-n+1} \cdots i_p j_{1+n} \cdots j_q} \; (\underline\delta_{i_1} \otimes \cdots \otimes \underline\delta_{i_{p-n}} \otimes \underline\delta^{j_{1+n}} \otimes \cdots \otimes \underline\delta^{j_q}) \\ &= \mathbf{A} \end{align}
- Introduction - Produit tensoriel - Produit tensoriel contracté
miniature
Des particules de lumière "filmés" dans leur déplacement 🎬
miniature
Montre moi tes mains, je te dirai quel buveur d'alcool tu es 🍺
miniature
Ces papillons interprètent les "cris" des plantes pour choisir où pondre 🦋
miniature
3
Le nombre d'articles scientifiques rétractés est en hausse ❌
miniature
Une nouvelle manière de lire les mémoires magnétiques 🧲
miniature
2
Vous êtes né avant 1986 ? Voici pourquoi vous risquez de développer des troubles psychiques ⚠️
miniature
Ce nouveau modèle relie matière noire et inflation cosmique 🌀
miniature
Ils ont rendu ce bois bioluminescent: vers un nouveau mode d'éclairage ? 💡
miniature
Des mouches dans la station spatiale chinoise Tiangong 🛰️
miniature
Cette main-robot nanométrique est capable de saisir des virus (exemple avec la COVID-19) 🖐️
miniature
1
Une étoile dévorée à pleine vitesse par... un trou noir ? 🌟
miniature
Cette astuce simple réduit la consommation d'alcool... des femmes 🍷
miniature
Découverte: la lumière transforme un isolant en métal 💡
miniature
1
Cet aliment à bannir nourrit les cancers 🍽️
miniature
Cette tablette de 3000 ans dévoile une écriture jusqu'alors inconnue ✍️
miniature
Découverte d'une chimie des océans refroidissant le climat 🌊
miniature
Le télescope James Webb, poussé à ses limites, découvre ces structures incroyablement anciennes 🔭
miniature
Le rôle surprenant de la grossesse contre la grippe A 🦠
miniature
Découverte d'une nouvelle espèce éteinte grâce à... un accélérateur de particules ⚛️
miniature
Une avancée prometteuse pour le déploiement des batteries sodium-ion 🔋
miniature
Voici comment et pourquoi le risque de cancer augmente... puis diminue avec l'âge 🧬
miniature
Le Soleil bientôt en "zone de combat": une période de turbulences extrêmes ☀️
miniature
1
Les rhumatismes plus douloureux par temps humide: vrai ou faux ? 🌧️
miniature
Ce nouveau type de moteur repousse les limites du vol supersonique ✈️
miniature
Poster sur les réseaux sociaux peut nuire à votre santé mentale 🧠
miniature
Une super-Terre entre Mars et Jupiter ? 🌎
miniature
Découverte impressionnante d'un fossile de crocodile géant 🐊
miniature
1
Cet accident en laboratoire pourrait transformer drastiquement la mémoire numérique ⚡
miniature
1
Un virage technologique révèle l'impact du diabète gestationnel 🩺
miniature
Insolite: ces loups butinent des fleurs ! Des grands carnivores pollinisateurs ? 🌼
miniature
1
Ce fin gilet robotisé soulage les tâches répétitives 🦾
miniature
Les équations d'Einstein invalidées ? 👀
miniature
Ce tatouage électronique se connecte à votre cerveau 🧠
miniature
Cette IA de Google prédit la météo mieux que jamais, et sur 15 jours ! 🌦️
miniature
Des plats au bœuf... sans bœuf ? 🥩
miniature
2
Ce moteur de recherche d'un nouveau genre bouscule nos habitudes 🔍
miniature
Pourquoi les cheveux bouclent-ils en fonction de la météo ? 🌦️
miniature
Découverte: d'autres univers plus propices à la vie que le notre 👽
miniature
Ces sons urbains qui minent notre santé mentale 🚗
miniature
La testostérone impacte-t-elle vraiment le désir sexuel des hommes ? 🔥
miniature
Des microalgues éliminent les métaux lourds: voici comment 🧪
miniature
1
Et voici un qubit mécanique ! 🖥️
miniature
Les lentilles de contact sont-elles vraiment sans danger ? 👁️
miniature
Dans la course à l'IA générative, Google lance son générateur de vidéos 🎥
miniature
4
Une zone oubliée du cerveau permet aux paralysés de marcher à nouveau 🧠
miniature
Cette astuce quotidienne ajoute 11 ans à votre vie 🕒
miniature
Révolutions, migrations des européens... les éruptions volcaniques ont influencé l'histoire 🌋
miniature
Soit l'énergie noire n'est pas constante, soit une seconde force inconnue est à l'œuvre... 🌀
miniature
Voici pourquoi l'alcool peut rendre agressif 🥂
miniature
Expérience inédite: ce laser projette une ombre visible 💥
Page générée en 0.060 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise