Localisation (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En algèbre, la localisation est une des opérations de base de l'algèbre commutative. C'est une méthode qui construit sur un anneau commutatif unitaire un nouvel anneau. La construction du corps des fractions est un cas particulier de la localisation.
Notion intuitive
La localisation consiste à rendre inversibles les éléments d'une partie ('partie multiplicative') de l'anneau. L'exemple le plus connu est le corps des fractions d'un anneau intègre qui se construit en rendant inversibles tous les éléments non-nuls de l'anneau. On peut aussi voir la localisation comme une manière d'envoyer l'anneau dans un anneau 'plus grand' dans lequel on a autorisé des divisions par des éléments qui n'étaient auparavant pas inversibles. Par exemple, le localisé de
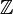
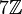
![\mathbb Z \left[ \frac 1 2 , \frac 1 3 , \frac 1 5 , \frac 1 {11} , \frac 1 {13}... \right]](https://static.techno-science.net/illustration/Definitions/autres/e/ef33bdfac77390fe16c3a5dbf58da6b9_89c65fa8dade52efc95d3e0ffb08f4be.png)
Construction
Pour construire l'anneau localisé, on procède comme dans la construction du corps des fractions mais avec une précaution supplémentaire pour tenir compte du fait que l'anneau n'est pas toujours intègre. Sur le produit cartésien

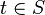
Définition
Soit A un anneau commutatif unitaire. On ne peut pas inverser un élément a ∈ A seul, car a-1a-1 est automatiquement l'inverse de a². On travaille donc avec une partie multiplicative, c'est-à-dire un ensemble
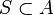
La localisation de l'anneau A en la partie S est alors la donnée d'un anneau, noté S -1A et d'un morphisme
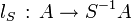

et qui vérifient la propriété universelle suivante : pour tout morphisme d'anneaux
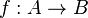
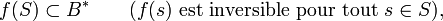
alors il existe un unique morphisme
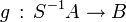
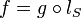
L'anneau S -1A est aussi noté AS ou A[S -1] et est appelé l'anneau des fractions de A associé à S, où à dénominateurs dans S, ou l'anneau des fractions de A par rapport à S.
Explication du terme localisation
Prenons l'anneau des polynômes ℂ[X]. Comme ℂ est algébriquement clos, le spectre d'anneau de ℂ[X] s'identifie à ℂ lui-même (avec un point supplémentaire correspondant à l'idéal nul). Le localisé en l'idéal maximal engendré par X, (X)= Xℂ[X], s'appelle le localisé en 0 et est précisément l'anneau des polynômes dans lequel on a autorisé toutes les divisions exceptées celles par les polynômes s'annulant en 0. Ce nouvel anneau est l'ensemble des fractions rationnelles sans pôle en 0 (donc holomorphes dans un voisinage de 0). Il permet de s'intéresser aux propriétés des polynômes au voisinage de 0, d'où le terme d'anneau localisé.
Exemples importants
- Les éléments réguliers (c'est-à-dire non diviseurs de zéro) forment une partie multiplicative notée
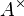
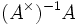
- Le complémentaire
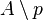
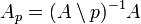
- Lorsque A est un anneau intègre, le premier exemple est un cas particulier du second. En effet, l'idéal nul est premier et son complémentaire est
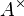
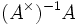
- Lorsque A est intègre, il est égal à l'intersection, dans son corps des fractions, de ses localisés en ses idéaux maximaux.
- Lorsque A n'est pas un anneau intègre, le complémentaire d'un idéal premier p peut contenir des diviseurs de zéros. L'homomorphisme de localisation
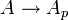
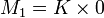
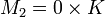
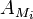
- Soit f un élément de A. L'ensemble S union de {1} et des puissances fn positives forment une partie multiplicative de A. La localisation de A par rapport à cette partie multiplicative est notée Af. Remarquons que Af est l'anneau nul si et seulement si f est nilpotent. Lorsque A est intègre, Af est l'ensemble des fractions qui peuvent s'exprimer comme le quotient d'un élément de A par une puissance positive de f.

















































