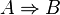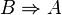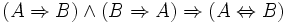Réciproque - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
La réciproque est une relation d'implication.
Si l'on a deux propositions A et B, voici les deux implications que l'on peut former à l'aide de ces propositions :
Ces implications sont réciproques l'une de l'autre : la première est la réciproque de la seconde et la seconde est la réciproque de la première.
Si on considère la première implication, A est une condition suffisante de B alors que si l'on considère la seconde, A est une condition nécessaire de B.
Lorsqu'une implication et sa réciproque sont vérifiées, il y a alors équivalence :
Exemple d'implication et de réciproque dans le langage courant :
- Si l'on considère les propositions suivantes : « Il y a du feu » et « Il y a de la fumée » alors :
- L'implication « S'il y a du feu, il y a de la fumée » a pour réciproque « S'il y a de la fumée, il y a du feu »
La contraposée est distingue de la réciproque.