Loi forte des grands nombres - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Loi forte des grands nombres de Kolmogorov
La moyenne empirique d’une suite de variables aléatoires indépendantes, identiquement distribuées, et intégrables, converge presque sûrement vers leur moyenne mathématique (ou espérance).
Autres formulations
On note souvent :
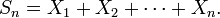
Ainsi l'énoncé devient
Théorème — Pour une suite  de v.a. i.i.d., on a :
de v.a. i.i.d., on a :
![\ \scriptstyle \left\{\text{p.s. }\tfrac{S_{n}(\omega)}{n}\text{ est une suite convergente}\right\}\Leftrightarrow\left\{\mathbb{E}\left[\left|X_{1}\right|\right]<+\infty\right\}.](https://static.techno-science.net/illustration/Definitions/autres/c/c100af4cd07cc455f7258296f0303814_70c2320ff3a9804eefcc4474d5884165.png)
De plus, si l'une de ces deux conditions équivalentes est remplie, on a:
![\ \scriptstyle \mathbb{P}\left(\omega\in\Omega\ \left|\ \lim_{n}\tfrac{S_{n}(\omega)}n=\mathbb{E}\left[X_{1}\right]\right.\right) = 1.](https://static.techno-science.net/illustration/Definitions/autres/c/cc3281f48e6983c95a0e70d1f500830c_fc77d73cfdfb6667d6459c02411dc217.png)
Énoncé usuel de la loi forte
L'énoncé ci-dessous est la forme habituelle de la loi forte des grands nombres, et est une conséquence directe (une forme affaiblie) du Théorème donné plus haut :
Théorème — Soit une suite
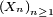
![\ \scriptstyle \mathbb{P}\left(\omega\in\Omega\ \left|\ \lim_{n}\tfrac{S_{n}(\omega)}n=\mathbb{E}\left[X_{1}\right]\right.\right) = 1.](https://static.techno-science.net/illustration/Definitions/autres/c/cc3281f48e6983c95a0e70d1f500830c_fc77d73cfdfb6667d6459c02411dc217.png)
Remarques
- En statistiques,
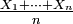
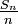
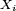
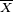
- On peut formuler l'hypothèse
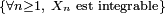
-
-
![\ \scriptstyle \left\{\forall n\ge1,\ \mathbb{E}\left[\left|X_{n}\right|\right]<+\infty\right\}\](https://static.techno-science.net/illustration/Definitions/autres/5/5abe38452309b13d48716f3d51b83c00_dd3f4f72c8dffc192cd2027723a894fb.png)
-
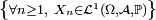
-
- ou bien encore, puisque les
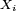
-
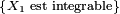
-
![\ \scriptstyle \left\{\mathbb{E}\left[\left|X_{1}\right|\right]<+\infty\right\}\](https://static.techno-science.net/illustration/Definitions/autres/6/6d16a7525f6c724e82e2b2699d33f239_d16c0f064b7f2f52c567afe9c1c99fa6.png)
-
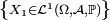
-

















































