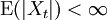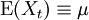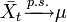Loi forte des grands nombres - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La loi forte des grands nombres est un énoncé mathématique énonçant que la moyenne d'une suite de variables aléatoires converge presque sûrement vers la même constante que l'espérance de la moyenne, sous certaines conditions (sur la dépendance, sur l'homogénéité et sur les moments).
Énoncé général
Le principe de la loi forte des grands nombres est que sous certaines conditions (sur la dépendance, sur l'homogénéité et sur les moments) la moyenne d'une suite de variables aléatoires {Xn} converge presque sûrement vers la même limite (constante) que l'espérance de la moyenne. En particulier, l'adjectif "fort" fait référence à la nature de la convergence établie par ce théorème : il est réservée à un résultat de convergence presque sûre. Par opposition, la loi faible des grands nombres, établie par Bernoulli, est un résultat de convergence en probabilité, seulement. Soit:
Principe général —
![\bar X_n -\bar\mu_n \xrightarrow{p.s.} 0\qquad \qquad \text{ avec } \bar X_n\equiv n^{-1}\sum_{i=1}^n X_i\text{ et } \bar \mu_n\equiv \operatorname{E}\left[\bar X_n\right]](https://static.techno-science.net/illustration/Definitions/autres/e/e54b9fc0d3aaadecec81b09b9ac3026b_2e921568efa67bad233fc87bd2e10cc4.png)
Il existe différents théorèmes selon le type d'hypothèses faites sur la suite {Xn} :
- observations indépendantes et identiquement distribuées,
- observations indépendantes et non-identiquement distribuées,
- observations dépendantes et identiquement distribuées.
Observations indépendantes et identiquement distribuées
Loi forte des grands nombres (Kolmogorov, 1929) — Si  est une suite de v.a. i.i.d., on a équivalence entre:
est une suite de v.a. i.i.d., on a équivalence entre:
-
- (i)
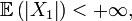
- (i)
-
- (ii) la suite
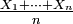
- (ii) la suite
- De plus, si l'une de ces deux conditions équivalentes est remplie, alors la suite
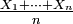
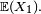
C'est la première loi forte à avoir été démontrée avec des hypothèses optimales. Pour la démontrer, il fallait définir rigoureusement le concept de convergence presque sûre, ce qui a amené Kolmogorov à considérer les probabilités comme une branche de la théorie de la mesure: saut conceptuel dont Kolmogorov prouvait ainsi l'efficacité. La théorie moderne des probabilités s'est construite à partir du travail fondateur de Kolmogorov sur la loi forte des grands nombres. La loi forte des grands nombres est aussi un ingrédient important dans la démonstration d'autres lois fortes des grands nombres, comme la LFGN pour les processus de renouvellement, ou la LFGN pour les chaînes de Markov. C'est de ce théorème qu'on parle lorsqu'on dit "la loi forte des grands nombres", les autres théorèmes n'étant que des lois fortes des grands nombres. Ce théorème est aussi intéressant parce qu'il aboutit à une conclusion plus forte : il établit l'équivalence entre l'intégrabilité de la suite et sa convergence, alors que les autres théorèmes fournissent seulement des implications, sans leurs réciproques. Dans le cas où les termes de la somme sont des variables de Bernoulli, la loi forte des grands nombres a été établie par Émile Borel en 1909. D'autres versions de la loi forte des grands nombres ont succédé à la version due à Borel, jusqu'à la version définitive de Kolmogorov.
Observations indépendantes et non-identiquement distribuées
Théorème de Markov — Soit {Xn} une suite de variables aléatoires indépendantes d'espérance finie
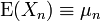
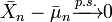
Pour pouvoir relacher l'hypothèse d'équidistribution, on est amené à faire une hypothèse plus forte sur l'intégrabilité.
Observations dépendantes et identiquement distribuées
Théorème ergodique — Soit {Xt} une suite de variables aléatoires stationnaire ergodique avec