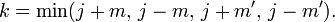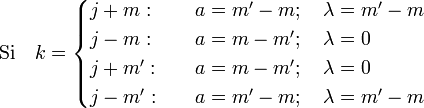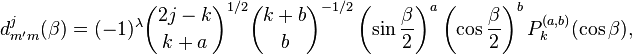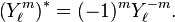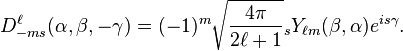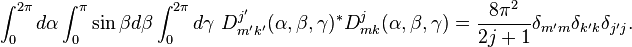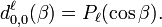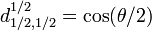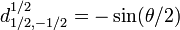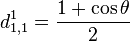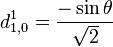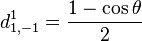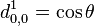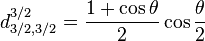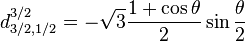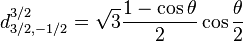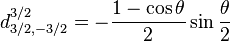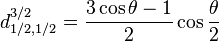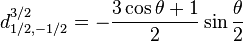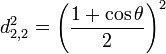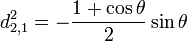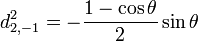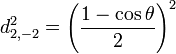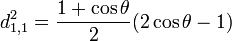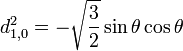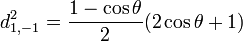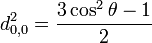Jeudi 1er Mai 2025
Rechercher 🔍

Matrice D de Wigner - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Définition de la matrice D de Wigner - Propriétés de la matrice D de Wigner - Matrice d de Wigner - Relation avec les fonctions harmoniques sphériques - Relation d'orthogonalité - Relation avec les fonctions de Bessel - Relation avec les polynômes de Legendre - Table des éléments de matrice d

Matrice d de Wigner

E. Wigner en donna l'expression suivante

\begin{array}{lcl} d^j_{m'm}(\beta) &=& [(j+m')!(j-m')!(j+m)!(j-m)!]^{1/2} \sum_s \frac{(-1)^{m'-m+s}}{(j+m-s)!s!(m'-m+s)!(j-m'-s)!} \\ &&\times \left(\cos\frac{\beta}{2}\right)^{2j+m-m'-2s}\left(\sin\frac{\beta}{2}\right)^{m'-m+2s}. \end{array}

La somme sur s est effectuée sur des valeurs telles que les factoriels ne soient pas négatifs.

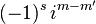
Note : les éléments de la matrice d définie ici sont réels. Dans la convention z-x-z des angles d'Euler parfois utilisée, le facteur ( − 1)m' − m + s de cette formule est remplacé par (-1)^s\, i^{m-m'} , ce qui implique que la moitié des fonctions soient purement imaginaires. La réalité (au sens mathématique) des éléments de la matrice d est l'une des raisons pour lesquelles la convention z-y-z, utilisée ici, est habituellement préférée dans les applications de mécanique quantique.

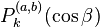
Les éléments de la matrice d sont reliés aux polynômes de Jacobi P^{(a,b)}_k(\cos\beta) avec a\, et b\, non-négatifs. Soit

k = \min(j+m,\,j-m,\,j+m',\,j-m').
\hbox{Si}\quad k = \begin{cases} j+m: &\quad a=m'-m;\quad \lambda=m'-m\\ j-m: &\quad a=m-m';\quad \lambda= 0 \\ j+m': &\quad a=m-m';\quad \lambda= 0 \\ j-m': &\quad a=m'-m;\quad \lambda=m'-m \\ \end{cases}

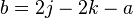
Donc, avec b=2j-2k-a\, , la relation est :

d^j_{m'm}(\beta) = (-1)^{\lambda} \binom{2j-k}{k+a}^{1/2} \binom{k+b}{b}^{-1/2} \left(\sin\frac{\beta}{2}\right)^a \left(\cos\frac{\beta}{2}\right)^b P^{(a,b)}_k(\cos\beta),

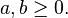
où a,b \ge 0. \,

Relation avec les fonctions harmoniques sphériques

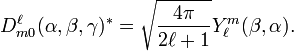
Les éléments de matrice D avec un second indice égal à 0 sont proportionnels aux Harmoniques sphériques, normalisées à l'unité et avec la convention de phase de Condon et Shortley :: D^{\ell}_{m 0}(\alpha,\beta,\gamma)^* = \sqrt{\frac{4\pi}{2\ell+1}} Y_{\ell}^m (\beta, \alpha ) .

Dans la convention actuelle des angles d'Euler, α est un angle longitudinal et β est un angle colatitudinal (angles polaires sphériques dans la définition physique de tels angles). C'est l'une des raisons pour lesquelles la convention z-y-z est utilisée fréquemment en physique moléculaire. De la propriété de réversibilité temporelle de la matrice D de Wigner il s'ensuit immédiatement :

\left( Y_{\ell}^m \right) ^* = (-1)^m Y_{\ell}^{-m}.

Il existe une relation plus générale avec les harmoniques sphériques pondérées par le spin :

D^{\ell}_{-m s}(\alpha,\beta,-\gamma) =(-1)^m \sqrt\frac{4\pi}{2{\ell}+1} {}_sY_{{\ell}m}(\beta,\alpha) e^{is\gamma}.

Relation d'orthogonalité

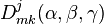
Les éléments de la matrice D de Wigner D^j_{mk}(\alpha,\beta,\gamma) constituent un ensemble complet de fonctions orthogonales des angles d'Euler α, β, et γ :

\int_0^{2\pi} d\alpha \int_0^\pi \sin \beta d\beta \int_0^{2\pi} d\gamma \,\, D^{j'}_{m'k'}(\alpha,\beta,\gamma)^\ast D^j_{mk}(\alpha,\beta,\gamma) = \frac{8\pi^2}{2j+1} \delta_{m'm}\delta_{k'k}\delta_{j'j}.

C'est un cas spécial des relations d'orthogonalité de Schur.

Relation avec les fonctions de Bessel

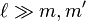
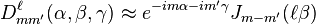
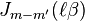
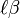
Dans la limite de \ell \gg m, m^\prime , on a D^\ell_{mm^\prime}(\alpha,\beta,\gamma) \approx e^{-im\alpha-im^\prime\gamma}J_{m-m^\prime}(\ell\beta) où J_{m-m^\prime}(\ell\beta) est la fonction de Bessel et \ell\beta est fini.

Relation avec les polynômes de Legendre

Les éléments de la matrice d de Wigner avec les deux indices à 0 sont liés aux polynômes de Legendre :

d^{\ell}_{0,0}(\beta) = P_{\ell}(\cos\beta).

Table des éléments de matrice d

En utilisant la convention de signe de Wigner et al., les éléments de matrice d pour j=1/2, 1, 3/2, et 2 sont donnés ci-dessous.

Pour j=1/2

  • d_{1/2,1/2}^{1/2} = \cos (\theta/2)
  • d_{1/2,-1/2}^{1/2} = -\sin (\theta/2)

Pour j=1

  • d_{1,1}^{1} = \frac{1+\cos \theta}{2}
  • d_{1,0}^{1} = \frac{-\sin \theta}{\sqrt{2}}
  • d_{1,-1}^{1} = \frac{1-\cos \theta}{2}
  • d_{0,0}^{1} = \cos \theta

Pour j=3/2

  • d_{3/2,3/2}^{3/2} = \frac{1+\cos \theta}{2} \cos \frac{\theta}{2}
  • d_{3/2,1/2}^{3/2} = -\sqrt{3} \frac{1+\cos \theta}{2} \sin \frac{\theta}{2}
  • d_{3/2,-1/2}^{3/2} = \sqrt{3} \frac{1-\cos \theta}{2} \cos \frac{\theta}{2}
  • d_{3/2,-3/2}^{3/2} = - \frac{1-\cos \theta}{2} \sin \frac{\theta}{2}
  • d_{1/2,1/2}^{3/2} = \frac{3\cos \theta - 1}{2} \cos \frac{\theta}{2}
  • d_{1/2,-1/2}^{3/2} = - \frac{3\cos \theta + 1}{2} \sin \frac{\theta}{2}

Pour j=2

  • d_{2,2}^{2} = \left(\frac{1+\cos \theta}{2}\right)^2
  • d_{2,1}^{2} = - \frac{1 + \cos \theta}{2} \sin \theta
  • d_{2,-1}^{2} = - \frac{1 - \cos \theta}{2} \sin \theta
  • d_{2,-2}^{2} = \left(\frac{1-\cos \theta}{2}\right)^2
  • d_{1,1}^{2} = \frac{1+\cos \theta}{2} (2 \cos \theta - 1)
  • d_{1,0}^{2} = -\sqrt{\frac{3}{2}} \sin \theta \cos \theta
  • d_{1,-1}^{2} = \frac{1-\cos \theta}{2} (2 \cos \theta + 1)
  • d_{0,0}^{2} = \frac{3 \cos^2 \theta - 1}{2}

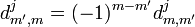
Les éléments de matrice d de Wigner avec les indices les plus faibles intervertis sont calculés avec la relation : d_{m', m}^j = (-1)^{m-m'}d_{m, m'}^j .

Propriétés de la matrice D de Wigner
- Introduction - Définition de la matrice D de Wigner - Propriétés de la matrice D de Wigner - Matrice d de Wigner - Relation avec les fonctions harmoniques sphériques - Relation d'orthogonalité - Relation avec les fonctions de Bessel - Relation avec les polynômes de Legendre - Table des éléments de matrice d
miniature
Une éruption volcanique en 2018 responsable d'une explosion de vie 🌋
miniature
Un système d'exploitation pour les ordinateurs quantiques voit le jour 🖥️
miniature
Des singularités temporelles dans l'Univers ? 🕰️
miniature
Des fossiles de dinosaures mieux datés 🦖
miniature
Une gigantesque muraille de 10 milliards d'années-lumière dans l'Univers 🔭
miniature
Benchmark: les processeurs quantiques sous la loupe, quels sont les meilleurs ? 🏆
miniature
Découverte d'une "fourmi de l'enfer" vieille de 113 millions d'années 🐜
miniature
Le rôle méconnu de la décharge dans l'usure des batteries 🔋
miniature
1
La fonte des glaces déplace les pôles: quelles conséquences ? 🌍
miniature
L'appareil photo de votre smartphone peut détecter l'antimatière 📱
miniature
Cette étoile-zombie peut déformer les atomes à distance, et elle fonce dans notre galaxie ⭐
miniature
Un mosasaure géant découvert dans le Mississippi 🦕
miniature
Problème, les galaxies meurent plus tôt que prévu 🌀
miniature
Ce lien entre cannabis et troubles psychotiques 🧠
miniature
Une révolution dans le refroidissement des puces électroniques ? 🔥
miniature
Des parasites sous-marins filmés en train de vampiriser un poisson des abysses 👀
miniature
Lucy survole un astéroïde en forme de cacahuète 🚀
miniature
Découverte du fossile d'un dinosaure géant méconnu 🦕
miniature
Mars avait-elle un champ magnétique unilatéral ? 🔍
miniature
Des chimpanzés surpris à sociabiliser avec de l'alcool 🍇
miniature
Découverte macabre: ce gladiateur a été tué par un lion il y a 1 800 ans... en Grande-Bretagne 🦁
miniature
L'électroluminescence du graphène, une découverte inattendue ! 💡
miniature
Cet objet métallique n'a pas été fabriqué sur Terre 🔧
miniature
1
Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡
miniature
Cette super-Terre brûle les attentes des astronomes 🔥
miniature
Découverte exceptionnelle de fossiles d'amphibiens géants 🐸
miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
miniature
Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷
miniature
Des puces quantiques plus proches que jamais ⚡
miniature
1
Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬
miniature
En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊
Page générée en 0.098 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise