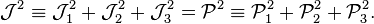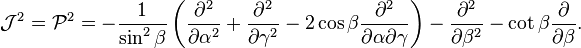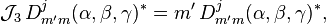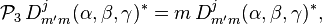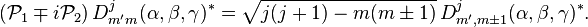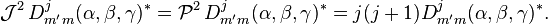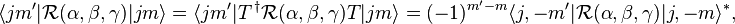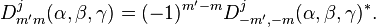Matrice D de Wigner - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La matrice D de Wigner est une matrice d'une représentation irréductible des groupes SU(2) et SO(3). Le conjugué complexe de la matrice D est une fonction propre du hamiltonien des rotateurs rigides sphériques et symétriques. Cette matrice fut introduite en 1927 par Eugene Wigner.
Définition de la matrice D de Wigner
Soient jx, jy, jz des générateurs d'une algèbre de Lie de SU(2) et SO(3). En mécanique quantique ces trois opérateurs sont les composantes d'un opérateur vectoriel appelé moment angulaire. On peut citer comme exemple le moment angulaire d'un électron dans un atome, le spin, ou le moment angulaire d'un rotateur rigide. Dans tous les cas, les trois opérateurs satisfont aux relations de commutation suivantes :
où i est un nombre imaginaire pur et la constante de Planck

est un opérateur de Casimir de SU(2) (ou SO(3) selon les cas). Il peut être diagonalisé avec jz (le choix de cet opérateur est une convention), qui commute avec j2. Ceci étant, on peut montrer qu'il existe un ensemble complet de kets avec :
où
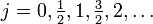
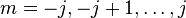
Un opérateur de rotation peut être écrit de la façon suivante :
où
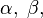
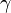
La matrice D de Wigner est une matrice carrée de dimension 2j + 1 avec pour élément général :
La matrice avec l'élément général :
est connue sous le nom de matrice d de Wigner (lire matrice petit d).
Propriétés de la matrice D de Wigner
Le complexe conjugué de la matrice D satisfait à un ensemble de propriétés différentielles qui peuvent être formulées de manière concise par l'introduction des opérateurs suivants avec
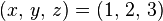
qui ont une signification en mécanique quantique : ce sont des opérateurs de moment angulaire pour un rotateur rigide fixe dans l'espace.
De plus,
qui ont une signification en mécanique quantique : ce sont des opérateurs de moment angulaire pour un rotateur rigide à référentiel lié.
Les opérateurs satisfont aux relations de commutation :
et ax relations correspondantes par permutation circulaire des indices.
Les

Les deux ensembles commutent mutuellement :
et les opérateurs totaux au carré sont égaux :
Leur forme explicite est :
Les opérateurs
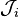
et
Les opérateurs

et en raison de la relation de commutation anomale, les opérateurs d'augmentation/de minimisation sont définis avec des signes inversés :
Enfin,
En d'autres termes, les lignes et colonnes de la matrice D de Wigner (conjugué complexe) couvrent les représentations irréductibles de l'algèbre de Lie isomorphe générée par
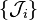
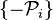
Une propriété importante de la matrice D de Wigner découle de la commutation de
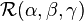

ou
Ici, on a utilisé le fait que

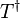
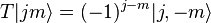
![[j_x,j_y] = i j_z,\quad [j_z,j_x] = i j_y,\quad [j_y,j_z] = i j_x,](https://static.techno-science.net/illustration/Definitions/autres/b/bd0e7da62570933a106bc92848581ee2_8ca5a6fd11c2d7fff1f826b7009e698c.png)
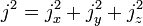
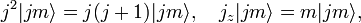
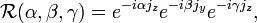
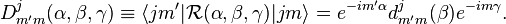
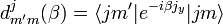
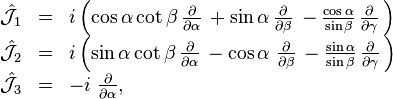
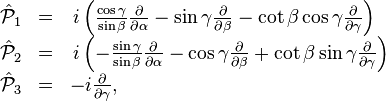
![\left[\mathcal{J}_1, \, \mathcal{J}_2\right] = i \mathcal{J}_3, \qquad \hbox{et}\qquad \left[\mathcal{P}_1, \, \mathcal{P}_2\right] = -i \mathcal{P}_3](https://static.techno-science.net/illustration/Definitions/autres/d/d763f99a923af00174d6c3a94ca0e28b_58c217e67dcbbef75a21996df7eaa060.png)
![\left[\mathcal{P}_i, \, \mathcal{J}_j\right] = 0,\quad i,\,j = 1,\,2,\,3,](https://static.techno-science.net/illustration/Definitions/autres/6/69e59d80c9045fd29fb02132c072baae_8ca8bafbe712bb0d0b50b52c8f657ba9.png)