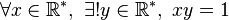Notation (mathématiques) - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Quantificateurs
Voir calcul des prédicats pour un point de vue plus théorique sur ces notations.
Pour tout
Notation

Exemples
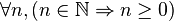
-
- Quel que soit n entier naturel, n est supérieur ou égal à zéro.
-

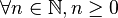
-
- Forme condensée.
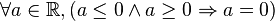
-
- Pour tout réel a, si a est inférieur ou égal à zéro, et si a est supérieur ou égal à zéro, alors a est nul.
- Tout réel, à la fois supérieur ou égal à zéro et inférieur ou égal à zéro, est nul.
Il existe
Notation
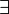
Exemples
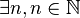
-
- Il existe un élément dans

-

- Il existe un élément dans
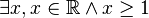
-
- Il existe un réel x tel que x soit plus grand ou égal à un.
-

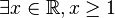
-
- Forme condensée.
Exemples généraux
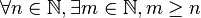
-
- Pour tout entier naturel n, il existe un autre entier naturel m tel que m soit supérieur ou égal à n.
- Tout entier naturel est inférieur ou égal à au moins un autre entier naturel.
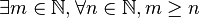
-
- Il existe un entier naturel m tel que quel que soit l'entier naturel n, m soit plus grand que n.
-

- On notera donc que l'ordre des quantificateurs est important : la première proposition est vraie, l'autre est fausse.
![\forall (a,l)\in\mathbb{R}^2, \exists f : \mathbb{R} \rightarrow \mathbb{R}, \forall \epsilon \in \mathbb{R_+^*}, \exists \alpha\in\mathbb{R_+^*}, \forall x\in[a-\alpha,a+\alpha], |f(x)-l|\le\epsilon](https://static.techno-science.net/illustration/Definitions/autres/b/bdc4ee9d572b4ded9f3a0d54c65a2882_2e7c27377c35ce40b27422f39a3a5799.png)
-
- Pour tout réels a et l, il existe une application f de


- Pour tout réels a et l, il existe une application f de
- Les quantificateurs permettent de définir les notions mathématiques.
Il existe un unique
La notation
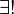
- ∃! x P(x) équivaut par définition à ∃ x [P(x) ∧ ∀ y (P(y) ⇒ y = x)]
ou de façon équivalente :
- ∃! x P(x) équivaut à ∃ x P(x) ∧ ∀ x ∀ y [(P(x) ∧ P(y)) ⇒ y = x] .
Exemple.