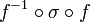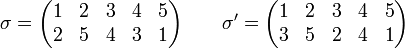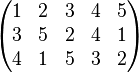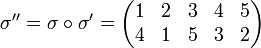Permutation - Définition

Propriétés algébriques

Composition de permutations

Les permutations de E sont définies comme des applications de E dans E, il est donc possible de définir leur produit de composition, qui se note (mais ce signe est le plus souvent omis). Précisément, pour deux permutations σ et σ', appliquer σ' puis σ revient à appliquer une permutation appelée le produit de σ et σ'.

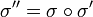
La notation des permutations est bien adaptée au calcul du produit de composition. Ainsi en prenant par exemple

Le calcul du produit peut être présenté sur trois lignes. La première et la deuxième ligne présentent l'effet de la première permutation σ', puis on fait correspondre aux éléments de la deuxième ligne leur image par σ.

Soit, finalement, en rayant la ligne de calcul intermédiaire

Il est à rappeler que la loi de composition n'est pas commutative.

Structure de groupe

Soient n éléments distincts dans un certain ordre. Appliquer une permutation σ revient à en modifier l'ordre. Revenir à l'ordre initial se fait aussi par une permutation ; celle-ci est notée σ^-1. Plus généralement, cette application σ^-1, est l'application réciproque de la bijection σ, puisqu'appliquer σ puis σ^-1 revient à appliquer la permutation identique. La permutation σ^-1 s'appelle la permutation réciproque ou permutation inverse de σ.

Soit E un ensemble quelconque. L'ensemble des permutations de E est un groupe pour la loi de composition , appelé groupe symétrique de E. Dans le cas particulier où avec , cet ensemble se note .

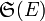
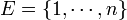
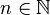
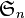
Si nous considérons un ensemble fini E (formé d'éléments qui ne sont pas nécessairement des entiers) de cardinal , nous pouvons numéroter les éléments de E et identifier les permutations des éléments de E avec les permutations des n premiers entiers.

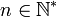
Démonstration formelle

Numéroter revient à introduire une application bijective . Il est alors possible d'associer à une permutation σ de , la permutation de E définie par . Nous obtenons ainsi une correspondance biunivoque (bijection) entre l'ensemble des permutations de et celui des permutations de E. Nous pouvons alors interpréter la permutation de précédente comme l'application (bijective) qui envoie l'élément f ^{− 1}(1) sur l'élément f ^{− 1}(2), l'élément f ^{− 1}(2) sur l'élément f ^{− 1}(3), et ainsi de suite.

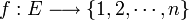
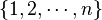
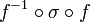
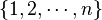
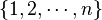
Plus précisément l'application qui à σ associe est un isomorphisme de groupes.