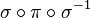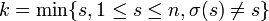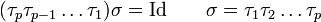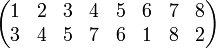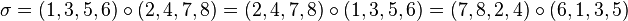Permutation - Définition

Décompositions des permutations

Décomposition en produit de transpositions

Toute permutation de support fini peut être décomposée en un produit de transpositions. Par exemple, cela signifie qu'on peut, par des échanges deux à deux, modifier à volonté l'ordre des cartes d'un paquet.

Une telle décomposition n'est pas unique : on peut par exemple ajouter un échange de deux cartes, puis l'échange des deux mêmes cartes. En revanche on démontre que la parité du nombre de transpositions nécessaire reste la même. Ceci permet de définir la parité et la signature d'une permutation (voir groupe symétrique).

Une permutation paire est une permutation qui peut être exprimée comme le produit d'un nombre pair de transpositions. Une définition équivalente est que sa décomposition en cycles disjoints donne un nombre pair (éventuellement nul) de cycles pairs. Une permutation impaire est une permutation qui peut être exprimée comme produit d'un nombre impair de transpositions.

La permutation identique est une permutation paire car elle peut être considérée comme le produit de 0 transposition, selon la convention sur le produit vide.

Algorithme de décomposition

Voici l'étape générale de l'algorithme de décomposition d'une permutation σ de support fini. On peut supposer que .

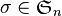
• si la permutation est l'identité elle est produit de 0 transposition.
• sinon il est possible de considérer le premier point non fixe par σ

Alors en appelant τ la transposition qui échange k et σ(k), on forme et on reprend l'algorithme avec σ₁.

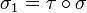
On forme ainsi des permutations σ₁, σ₂ etc. obtenues en multipliant σ par une succession de transpositions τ₁, τ₂ etc., jusqu'à atteindre la permutation identique. Alors il vient

La validité de l'algorithme se justifie en remarquant que la position du premier point non fixe augmente strictement à chaque étape, jusqu'à ce que tous les points soient fixes. L'algorithme se conclut après au plus n-1 opérations, puisque si les n-1 premiers points sont fixes, ils le sont tous.

Ainsi il est possible d'affirmer plus précisément que toute permutation peut s'écrire comme produit d'au plus n-1 transpositions. En outre, le nombre minimum de transpositions nécessaires pour écrire une permutation donnée est exactement celui obtenu avec cet algorithme.

Décomposition en produit de cycles à supports disjoints

Orbite d'un élément

les deux cycles de la permutation σ

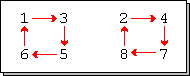
L'orbite d'un élément selon une permutation σ est l'ensemble de ses images successives obtenues par applications répétées de σ. Ainsi en introduisant la permutation σ

L'élément 1 a pour images successivement 3,5,6 puis de nouveau 1,3,5 etc. L'orbite de 1 est donc l'ensemble {1,3,5,6}. L'orbite de 3 est également l'ensemble {1,3,5,6}, mais l'orbite de 2 est {2,4,7,8}.

Plus généralement, pour une permutation quelconque, les orbites sont disjointes et forment une partition de l'ensemble {1,2,...,n}. En restriction à une orbite donnée de taille p, la permutation se comporte comme une permutation circulaire des p éléments.

Décomposition

Pour décrire la permutation, il suffit de prendre un élément dans chaque orbite et de donner l'ordre de succession de ses images par itération de σ. Ainsi toujours avec le même exemple, la permutation σ peut s'écrire sous la forme d'une succession des deux cycles (1,3,5,6) et (2,4,7,8). L'ordre des cycles n'importe pas mais l'ordre des éléments à l'intérieur d'un cycle doit être respecté jusqu'à l'obtention d'un cycle complet. Ainsi, la même permutation peut être écrite par exemple

Dans cette notation on omet souvent le symbole de composition pour alléger l'écriture.

La décomposition « canonique » d'une permutation en « produit » de cycles s'obtient en plaçant d'abord le plus petit nombre en première position dans chaque cycle et en ordonnant les cycles selon leur premier élément. Cette notation omet souvent les points fixes, c'est-à-dire les éléments qui sont leur propre image par la permutation; ainsi la permutation (1 3)(2)(4 5) s'écrit simplement (1 3)(4 5), puisqu'un cycle d'un seul élément n'a aucun effet.

Si, au contraire, on place le plus petit nombre en dernière position dans chaque cycle, sans omettre les points fixes, on obtient une suite de nombres, liée aux nombres de Stirling, qui permet l'analyse combinatoire du nombre de cycles et de la taille des cycles d'une permutation : c'est la correspondance fondamentale de Foata.

Applications

De nombreuses propriétés de la permutation σ peuvent se lire facilement sur la décomposition en cycles disjoints : s'il y a p cycles de longueurs s₁, ..., s_p (en comptant les points fixes comme cycles de longueur 1)

• la signature de σ est le produit des signatures : elle vaut (-1)^n-p=(-1)^p', où p' est le nombre de cycles de longueur paire.
• l'ordre de σ (en tant que membre du groupe symétrique) est le plus petit entier k>0 tel que σ^k est l'identité. Il est égal au PPCM des longueurs des cycles.
• le théorème des restes chinois est clairement illustré par les puissances de σ. Il est plus facile à énoncer quand les longueurs des cycles sont premières entre elles : l'ordre de σ est le produit des longueurs des cycles et le groupe engendré par les puissances de σ est isomorphe à qui lui même est décomposable en produit des , chaque cycle avançant à son rythme pour ne retomber en phase qu'au produit.
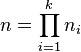
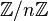
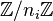
• la conjuguée d'une permutation π par une permutation σ est la permutation . On peut aisément calculer cette permutation, en remplaçant chaque élément i dans la décomposition en cycles disjoints de π par σ_i.