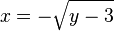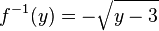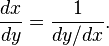Application réciproque - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, une application réciproque est en des termes simples une fonction qui « fait exactement l'inverse de ce que fait une application donnée ». L'application réciproque permet de retrouver un élément à partir de son image par une application donnée; autrement dit une application réciproque défait ce que l'application originale a fait. Toutes les applications ne possèdent pas d'application réciproque. Lorsque c'est le cas, on parle d'application « inversible ».
Exemple
On considère la fonction
Pour défaire ce qu'a fait f, on peut remarquer que f est composée de deux opérations élémentaires faciles à défaire
Ainsi, en appliquant à y, la fonction
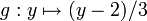
- Pour tout réel x,
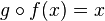
De même, en appliquant à un réel y la fonction g puis en appliquant au résultat la fonction f, on retrouve le réel y. En langage mathématique cela s'écrit :
- Pour tout réel y,
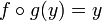
La fonction, définie sur un ensemble E, qui laisse invariants tous les éléments de E, se note IdE. Les égalités précédentes s'écrivent donc :
-
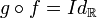
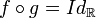
On dit alors que g est l'application réciproque de f et on la note f − 1
L'exposant « -1 » n'est pas une puissance et f − 1 ne correspond pas à l'inverse d'une fonction pour la multiplication, mais à l'inverse pour la composition de fonctions.
Réciproque d'une fonction numérique
Existence
Le théorème des valeurs intermédiaires et son corollaire, le théorème de la bijection, assurent que toute application continue strictement monotone sur un intervalle I détermine un bijection de I sur f(I) = J et que J est aussi un intervalle. Cela signifie qu'une telle fonction possède une application réciproque définie sur J à valeurs dans I.
Cette propriété permet la création de nouvelles fonctions définies comme application réciproque de fonctions usuelles.
Exemples
| Fonction f(x) | Départ et arrivée | Fonction réciproque | Départ et arrivée | Notes |
|---|---|---|---|---|
| f(x) = xn |
|
|
| n entier naturel non nul |
| f(x) = ex |
| f − 1(x) = ln(x) |
| |
| f(x) = ax |
| f − 1(x) = loga(x) |
| a réel strictement positif |
| f(x) = xα |
| f − 1(x) = x1 / α |
| α réel non nul |
| f(x) = sin(x) |
| f − 1(x) = arcsin(x) |
| |
| f(x) = cos(x) |
| f − 1(x) = arccos(x) |
| |
| f(x) = tan(x) |
| f − 1(x) = arctan(x) |
|
À l'aide de ces fonctions, la recherche de l'application réciproque consiste à résoudre l'équation f(x) = y, d'inconnue x :
La fonction
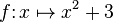
![]- \infty;0]](https://static.techno-science.net/illustration/Definitions/autres/6/6784e26006f1ff6da806742141c799e4_2524aa17193906f8c1f17fe6d38c995b.png)
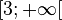
- x2 + 3 = y
pour y dans
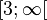
- x2 = y − 3
puisque
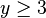
![]- \infty;0]](https://static.techno-science.net/illustration/Definitions/autres/6/6784e26006f1ff6da806742141c799e4_2524aa17193906f8c1f17fe6d38c995b.png)
Donc la réciproque de f est f − 1 définie par :
Cette recherche peut se révéler infructueuse et nécessiter la création d'une fonction nouvelle.
Graphe
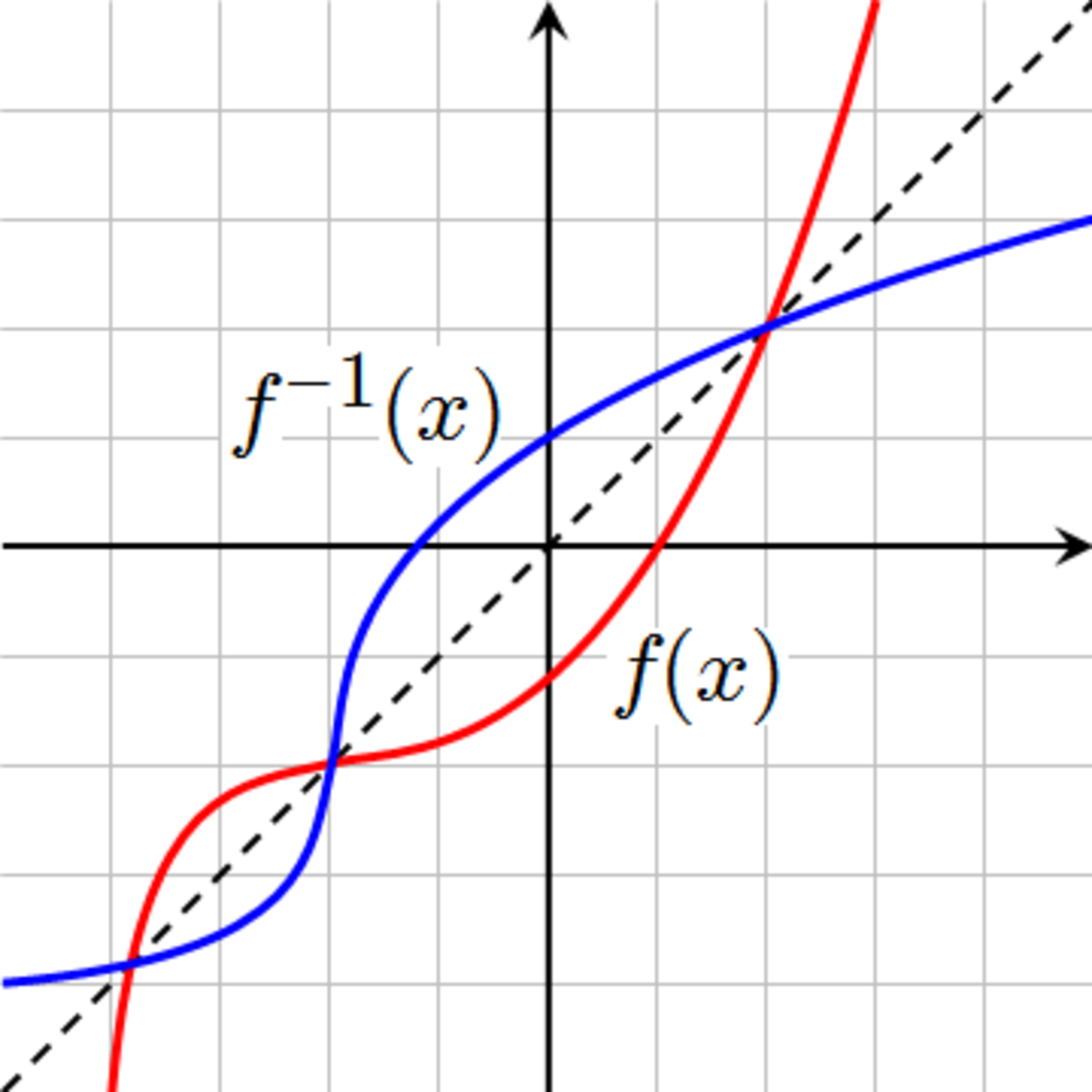
Lorsque deux fonctions sont réciproques l'une de l'autre alors leurs représentations graphiques dans un plan muni d'un repère orthonormal sont symétriques l'une de l'autre par rapport à la droite (d) d'équation y = x.
En effet, si M(x ; y) est un point du graphe de f alors y = f(x) donc x = f − 1(y) donc M'(y ; x) est un point du graphe de f − 1. Or le point M'(y ; x) est le symétrique du point M(x ; y) par rapport à (d) pour les deux raisons suivantes :
Le milieu du segment [M M'] est sur la droite d'équation y = x, et d'autre part, le vecteur
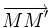
On sait donc que s(M) est un point du graphe de f − 1. Un raisonnement analogue prouve que si M est un point du graphe de f − 1 alors s(M) est un point du graphe de f.
Continuité
En général, la réciproque d'une fonction continue n'est pas continue mais la réciproque d'une fonction continue sur un intervalle I à valeurs dans un intervalle J est une fonction continue sur J. On trouve une démonstration dans l'article Théorème d'inversion locale.
Dérivabilité
Si f est une fonction continue sur un intervalle I à valeurs dans un intervalle J et si f − 1 est sa réciproque, la fonction f − 1 est dérivable en tout point b tant que f admet en f − 1(b) une dérivée non nulle. La dérivée en b de f − 1 est alors
-
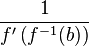
Un moyen simple de comprendre, mais non de démontrer, ce phénomène est d'utiliser les notations différentielles et de remarquer que :
On trouve une démonstration dans l'article Opérations sur les dérivées.
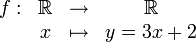
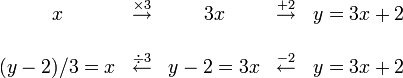
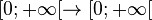
![f^{-1}(x)=\sqrt[n]x](https://static.techno-science.net/illustration/Definitions/autres/9/9030b4aecc1876a245c09813b346e198_fba0f7f86580be8979aff67605c59732.png)
![\R \to ]0;+ \infty[](https://static.techno-science.net/illustration/Definitions/autres/c/c17402df173139d0b0102ce6fa8d9214_1ed63c5f91f8c6f54f6f25d983388cd7.png)
![]0;+ \infty[\to \R](https://static.techno-science.net/illustration/Definitions/autres/d/d96a09cda41694ef9ea79589d0552939_35060945ffb743024e1cfbae36b25c4d.png)
![]0;+\infty[ \to ]0;+\infty[](https://static.techno-science.net/illustration/Definitions/autres/d/d7b057073dbc146440257be6475a1ca7_21b867b98f3609146e841b00b2dee2b5.png)
![[-\pi/2;\pi/2] \to [-1;1]](https://static.techno-science.net/illustration/Definitions/autres/c/ccf7f365f28d836d41574a1dcab1aebc_7bb585c3bb3cee72d421a1ec7c433319.png)
![[-1;1] \to [-\pi/2;\pi/2]](https://static.techno-science.net/illustration/Definitions/autres/e/e83d15853d3630dd8f2d49d95b4a26f8_f8c110b1f048e2bd21d459dbba9cd6b1.png)
![[0;\pi] \to [-1;1]](https://static.techno-science.net/illustration/Definitions/autres/e/e1dbd3c8da0f5055c1243b8dd2e56fca_f5ed87c1f46e8b98ea02ea363d15d0f4.png)
![[-1;1] \to [0;\pi]](https://static.techno-science.net/illustration/Definitions/autres/9/91ded40be1295ebba09a6ba2f251a4af_64c3507a1bbe3b893d9a15a8b4233e05.png)
![]-\pi/2;\pi/2[ \to \R](https://static.techno-science.net/illustration/Definitions/autres/c/cd86161afc330eb03b838d742c2ad208_f9e347aa92b0462607e6965840fcf52e.png)
![\R \to ]-\pi/2;\pi/2[](https://static.techno-science.net/illustration/Definitions/autres/2/23ff75e230232b2afcd1ebad5da7029a_959abc3ed1df1b69522676d2729c67d1.png)