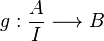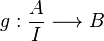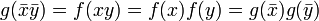Propriété universelle - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Propriété universelle : définition - Propriété universelle de la somme directe externe - Propriété universelle des modules quotients - Propriété universelle du produit - Propriété universelle des modules libres - Propriété universelle des corps des fractions - Propriété universelle des anneaux de fractions - Propriété universelle des groupes quotients - Propriété universelle des algèbres

Propriété universelle des groupes quotients

Cette propriété est similaire à celle des modules quotients.

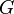
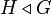
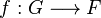
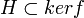
Soient $\displaystyle G$ et $\displaystyle F$ deux groupes, soit $H \triangleleft G$ Soit $f : G \longrightarrow F$ un morphisme de groupes tel que $H \subset ker f$ .

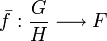
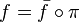
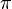
Alors il existe un unique morphisme de groupe $\bar f : \frac {G}{H} \longrightarrow F$ tel que $f = \bar f \circ \pi$ avec $\displaystyle \pi$ la surjection cannonique.

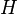
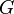
La démonstration de cette propriété est semblable à celle de la propriété universelle des modules quotients, sauf qu'on suppose dans les prémisses que $\displaystyle f$ est constante sur les classes. Par ailleurs, on introduit la normalité de $\displaystyle H$ dans $\displaystyle G$ pour ne pas avoir à énoncer la propriété pour le groupe quotient à gauche et pour le groupe quotient à droite.

Propriété universelle des algèbres

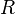
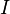
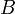
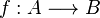
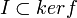
Soient $\displaystyle R$ un corps, $\displaystyle A$ une R-algèbre, $\displaystyle I$ un idéal bilatère de $\displaystyle A$ , $\displaystyle B$ une R-algèbre. Soit $f : A \longrightarrow B$ un morphisme d'algèbre tel que $I \subset ker f$ .

Alors il existe un unique morphisme d'algèbre $g : \frac A I \longrightarrow B$ tel que $g \circ \pi = f$ avec $\displaystyle \pi$ la surjection canonique.

$\displaystyle f$ est un morphisme de R-module. La propriété universelle des modules quotients assure qu'il existe $g : \frac A I \longrightarrow B$ R-linéaire tel que $g \circ \pi = f$ . Il suffit donc de montrer que $\displaystyle g$ est un morphisme d'algèbre :

Propriété universelle des anneaux de fractions

Cet objet métallique n'a pas été fabriqué sur Terre 🔧

Cette innovation permet aux voitures électriques de charger 6 fois plus vite par grand froid ⚡

Cette super-Terre brûle les attentes des astronomes 🔥

Découverte exceptionnelle de fossiles d'amphibiens géants 🐸

Voici ce qui a causé les toutes premières inégalités de richesse 💰

Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊

Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭

Des cellules solaires flexibles battent des records d'efficacité ⚡

Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀

Record établi pour un transistor en diamant 💎

Les sursauts radio rapides trahissent enfin leur origine cosmique 📡

Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠

Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊

Les oscillations collectives des foules humaines denses 🔁

Une forme inconnue de la matière détectée au LHC ? ⚛️

Le sel, un facteur méconnu de l'obésité ? 🧂

L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀

Découverte tectonique majeure sous les Petites Antilles 🌍

Peut-on geler en chauffant ? ❄️

Une peau électronique pour doter les robots du sens du toucher 👌

Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳

Le cancer inscrit dans nos gènes dès la naissance ? 🧬

Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥

Le passé verdoyant du plus grand désert du monde 🐪

Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷

Des puces quantiques plus proches que jamais ⚡

Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬

En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊

Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️

Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜

Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️

Cette vitamine développe les fonctions cognitives du cerveau 🧠

Comment des impacts géants vaporisent les corps planétaires ☄️

Les Américains riches vivent moins longtemps que les Européens pauvres 💰

Attention à ce riz naturellement riche en arsenic 🍚

L'intelligence artificielle contre la mort subite 💀

L'inévitable formation d'un océan de magma basal sur Terre 🔥

Découverte d'une plante étrange sans chlorophylle 🌱

Existe-t-il des mélodies naturelles ? 🎶

Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽

L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡

Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺

Imprimer en 3D avec la lumière du soleil ☀️

La pollution atmosphérique nuit gravement au cerveau 🧠

Le trou noir supermassif Ansky vient de se réveiller ⚫

Voici ce qui rend notre cerveau vraiment unique 🧠

Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩

Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬

La physique révèle les secrets d'un strike parfait au bowling 🎳

Le TDAH associé à la démence 🧠

Page générée en 0.086 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise