Propriété universelle - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, une propriété universelle est la propriété des objets qui sont la solution d'un problème universel posé par un foncteur.
Propriété universelle : définition
Soit







Pour tout objet





Le foncteur

Propriété universelle de la somme directe externe
Soit A un anneau ; soit


Alors il existe une unique application




Par analyse synthèse :
- Supposons qu'un tel
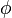







- Posons donc


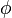



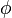
Propriété universelle des modules quotients
Soient
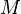


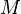

Alors il existe une unique application








Par analyse-synthèse :
- Supposons qu'une telle application

Soit





On a bien


- Supposons

Par analyse-synthèse :
Posons



soient







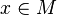



Propriété universelle du produit
Soit

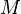

Alors il existe une unique application linéaire


avec

On a donc le diagramme suivant :

Par analyse-synthèse :
Posons

Soit
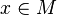


Soit





Propriété universelle des modules libres
Soit M un module libre de base
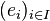
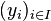
Alors il existe une unique application linéaire



Par analyse synthèse :
- Supposons qu'une telle application f existe. Soit
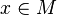



- Posons donc

f est linéaire, ce qui se démontre aisément ; soit
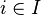

Propriété universelle des corps des fractions
Cette propriété universelle est un cas particulier de la propriété universelle des anneaux de fractions
Soit







Alors il existe un unique morphisme



Propriété universelle des anneaux de fractions
Soit








Alors il existe un unique morphisme




Par analyse-synthèse :
-

Or



Donc



- Posons

Montrons que







































































