Relation ternaire externe - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Une relation ternaire externe dans un ensemble associe des éléments de cet ensemble à des couples dont une composante vient de cet ensemble et l'autre d'un ensemble dit de scalaires ou d' opérateurs.
Définitions
Dans ce qui précède, une question se pose : les scalaires forment-ils la première ou la seconde composante des couples concernés ? Pour lever cette ambiguïté, il faut distinguer entre relations ternaires externes à gauche et à droite.
Plus précisément, une relation ternaire externe à gauche
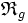
- l'ensemble de départ S×E;
- l'ensemble d'arrivée E;
- et un graphe G inclus dans S×E 2 , donc formé de triplets dont la première composante est scalaire et les deux autres sont des éléments de E.
Si λ est un élément de S, c'est-à-dire un scalaire, et x et y deux éléments de E, nous pouvons écrire que y est image par
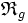
- ( λ , x , y ) ∈ G ( notation ensembliste )
- ( λ , x , y )
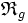
-
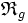
- ( λ , x )
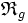
Nous utiliserons dans la suite cette dernière notation.
Symétriquement, une relation ternaire externe à droite
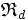
- l'ensemble de départ E×S;
- l'ensemble d'arrivée E;
- et un graphe G inclus dans E×S×E, donc formé de triplets dont la deuxième composante est scalaire et les deux autres sont des éléments de E.
Si λ est un élément de S, c'est-à-dire un scalaire, et x et y deux éléments de E, nous pouvons écrire que y est image par
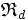
- ( x , λ , y ) ∈ G ( notation ensembliste )
- ( x , λ , y )
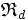
-
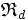
- ( x , λ )
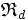
Là encore, nous utiliserons dans la suite cette dernière notation.
Cas particuliers :
- Une opération externe est une relation ternaire externe qui est aussi une fonction.
- Une loi de composition externe est une relation ternaire externe qui est aussi une application.
Relation ternaire opposée
Définition
Soit un ensemble E muni d'une relation ternaire externe

La relation ternaire opposée à


- - si la relation est à gauche :
-
- - si la relation est à droite :
-
Principales propriétés
Soit un ensemble E muni d'une relation ternaire externe

-


- ou :
- - pour une relation à gauche :
-
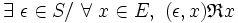
- - et à droite :
-
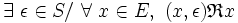
-


- ou :
- - pour une relation à gauche :
-
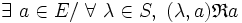
- - et à droite :
-
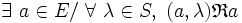
-


- ou :
- - pour une relation à gauche :
-
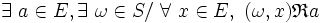
- - et à droite :
-
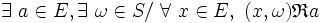
-

- ou :
- - pour une relation à gauche :
-
![\forall\ \lambda \in S , \forall\ ( x , y , z ) \in E^3 , [\ ( \lambda , x ) \mathfrak{R} z \ \wedge\ ( \lambda , y ) \mathfrak{R} z \ ] \Rightarrow ( x = y ) \,](https://static.techno-science.net/illustration/Definitions/autres/a/abc03637f9f4fa2c3d972acbde206240_0680bf8603c8681a30feb2e9f705054e.png)
- - et à droite :
-
![\forall\ \lambda \in S , \forall\ ( x , y , z ) \in E^3 , [\ ( x , \lambda ) \mathfrak{R} z \ \wedge\ ( y , \lambda ) \mathfrak{R} z \ ] \Rightarrow ( x = y ) \,](https://static.techno-science.net/illustration/Definitions/autres/8/831b4e3e4dfb30fcc5fb54bb375be6bb_df0d21d71f938fe529c4edb10a2b4772.png)
-

- ou :
- - pour une relation à gauche :
-
![\forall\ ( \lambda , \mu ) \in S^2 , \forall\ ( x , y ) \in E^2 , [\ ( \lambda , x ) \mathfrak{R} y \ \wedge\ ( \mu , x ) \mathfrak{R} y \ ] \Rightarrow ( \lambda = \mu ) \,](https://static.techno-science.net/illustration/Definitions/autres/d/d29c8828fdfb0f4958a9f1d9f5b743d2_2296df3643374d1a992bc26c01ff819e.png)
- - et à droite :
-
![\forall\ ( \lambda , \mu ) \in S^2 , \forall\ ( x , y ) \in E^2 , [\ ( x , \lambda ) \mathfrak{R} y \ \wedge\ ( x , \mu ) \mathfrak{R} y \ ] \Rightarrow ( \lambda = \mu ) \,](https://static.techno-science.net/illustration/Definitions/autres/f/ff21305f46a413651c898fb2c06d4e2d_cbb3f395af349e01a2b582e863cb36f3.png)
-


![\forall\ \lambda \in S , \forall\ ( x , y ) \in E^2 , \ [ \ ( x , \lambda ) ( - \mathfrak{R} ) y \ ] \Leftrightarrow [ \ ( \lambda , x ) \mathfrak{R} y \ ] \,](https://static.techno-science.net/illustration/Definitions/autres/8/89edfaff0825a6711b9c9453b63831e9_e78550dc429a920c22f6932e5219e475.png)
![\forall\ \lambda \in S , \forall\ ( x , y ) \in E^2 , \ [ \ ( \lambda , x ) ( - \mathfrak{R} ) y \ ] \Leftrightarrow [ \ ( x , \lambda ) \mathfrak{R} y \ ] \,](https://static.techno-science.net/illustration/Definitions/autres/d/d3e06998994fb531f4c6335569ca4c5e_a0823dd87d498a755b25375e9c1ee492.png)

















































