Relation ternaire externe - Définition
La liste des auteurs de cet article est disponible ici.
Relations inverses
Définitions
Soit un ensemble E muni d'une relation ternaire externe à gauche ( resp. à droite )
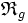
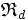
La relation inverse à gauche ( resp. à droite ) ( ou RIG ( resp. RID )) de la relation
-
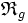
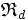
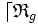
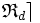
![\forall\ \lambda \in S , \forall\ ( x , y ) \in E^2 ,\ [\ ( x , y ) \lceil \mathfrak{R}_g \lambda\ ] \Leftrightarrow [\ ( \lambda , y ) \mathfrak{R}_g x \ ] \,](https://static.techno-science.net/illustration/Definitions/autres/8/851fd3128a995d814a1939fce82ee468_a2b1793f5f91319d92cda9dcff36bc55.png)
- ou resp. pour une relation à droite par :
-
![\forall\ \lambda \in S , \forall\ ( x , y ) \in E^2 ,\ [\ ( x , y ) \mathfrak{R}_d \rceil \lambda\ ] \Leftrightarrow [\ ( y , \lambda ) \mathfrak{R}_d x \ ] \,](https://static.techno-science.net/illustration/Definitions/autres/0/0e1b4fb4305101b9869249e4f940b826_68acb5528cf95402e238c99e991c38f0.png)
![\forall\ \lambda \in S , \forall\ ( x , y ) \in E^2 ,\ [\ ( x , y ) \lceil \mathfrak{R}_g \lambda\ ] \Leftrightarrow [\ ( \lambda , y ) \mathfrak{R}_g x \ ] \,](https://static.techno-science.net/illustrationWebp/Definitions/autres/8/851fd3128a995d814a1939fce82ee468_a2b1793f5f91319d92cda9dcff36bc55.png)
![\forall\ \lambda \in S , \forall\ ( x , y ) \in E^2 ,\ [\ ( x , y ) \mathfrak{R}_d \rceil \lambda\ ] \Leftrightarrow [\ ( y , \lambda ) \mathfrak{R}_d x \ ] \,](https://static.techno-science.net/illustrationWebp/Definitions/autres/0/0e1b4fb4305101b9869249e4f940b826_68acb5528cf95402e238c99e991c38f0.png)
La relation ternaire inverse à droite ( resp. à gauche ) ( ou RTID ( resp. RTIG ) de la relation
-
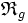
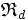
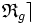
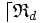
![\forall\ \lambda \in S , \forall\ ( x , y ) \in E^2 ,\ [\ ( x , \lambda ) \mathfrak{R}_g \rceil y \ ] \Leftrightarrow [\ ( \lambda , y ) \mathfrak{R}_g x \ ] \,](https://static.techno-science.net/illustration/Definitions/autres/7/796d4521e6e9e14082c8f20ef0e73480_eb517d6fe9898fefe1ac1571497dd582.png)
- ou resp. pour une relation à droite par :
-
![\forall\ \lambda \in S , \forall\ ( x , y ) \in E^2 ,\ [\ ( x , \lambda ) \lceil \mathfrak{R}_d y \ ] \Leftrightarrow [\ ( y , \lambda ) \mathfrak{R}_d x \ ] \,](https://static.techno-science.net/illustration/Definitions/autres/a/a745714aad9710992613f80a13e1e5ae_e55f2cddefa78ba24a954010ed954805.png)
![\forall\ \lambda \in S , \forall\ ( x , y ) \in E^2 ,\ [\ ( x , \lambda ) \mathfrak{R}_g \rceil y \ ] \Leftrightarrow [\ ( \lambda , y ) \mathfrak{R}_g x \ ] \,](https://static.techno-science.net/illustrationWebp/Definitions/autres/7/796d4521e6e9e14082c8f20ef0e73480_eb517d6fe9898fefe1ac1571497dd582.png)
![\forall\ \lambda \in S , \forall\ ( x , y ) \in E^2 ,\ [\ ( x , \lambda ) \lceil \mathfrak{R}_d y \ ] \Leftrightarrow [\ ( y , \lambda ) \mathfrak{R}_d x \ ] \,](https://static.techno-science.net/illustrationWebp/Definitions/autres/a/a745714aad9710992613f80a13e1e5ae_e55f2cddefa78ba24a954010ed954805.png)
Ces définitions peuvent sembler à première vue arbitraires, mais elles sont telles qu'elles coïncident avec les définitions des relations inverses pour les relations ternaires internes, dans le cas où S = E.
Propriétés
- Toute relation ternaire externe à droite est la RTIG de sa RTIG.
- La RTIG de l'opposée d'une relation ternaire externe à gauche est la RTID de cette dernière.
- La RID de l'opposée d'une relation ternaire externe à gauche est la RIG de cette dernière, et c'est une relation scalaire.
- La RTID de l'opposée d'une relation ternaire externe à droite est la RTIG de cette dernière.
- La RIG de l'opposée d'une relation ternaire externe à droite est la RID de cette dernière, et c'est une relation scalaire.
Propriétés
- Chaque relation ternaire externe a une relation opposée et une seule.
- La relation opposée d'une relation ternaire externe à gauche est une relation à droite, et vice versa.
- Toute relation ternaire est l'opposée de son opposée.
- L'opposée d'une relation ternaire est une opération ssi cette relation est une opération.
- L'opposée d'une relation ternaire est une loi de composition ssi cette relation est une loi de composition.
- Une relation ternaire externe n'est jamais égale à son opposée ( hormis le cas d'une relation interne , mais il s'agit alors d'un abus de langage ).
